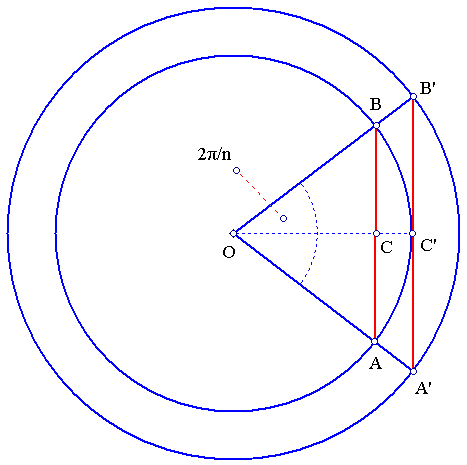
Archimedes estimated the area of the circle E, by using successive approximations with inscribed and circumscribed polygons. Here is a modern variant of this method. Consider a partition of the circle into n equal sectors, each sector subtending an angle of 2*π/n from the center. The key idea is that (OAB) < SectorArea(OAB) < (OA'B') and AB < ArcLength(AB) < A'B'.

Estimation of Area:

AB and OC, are:

AB=2*r*sin(π/n) and
OC=r*cos(π/n)

Therefore the triangle OAB has area:
1/2*2*r²*sin(π/n)*cos(π/n)=
r²/2*sin(2*π/n) =>
OAB=r²/2*sin(2*π/n)

The total area for the inscribed polygon then, will be given by LE=n*OAB, so a lower bound for the area of the circle will be:
LE=n*r²/2*sin(2*π/n) (1)

A'B' and OC', are:
A'B'=2*r*tan(π/n) and
OC'=r

therefore the triangle OA'B' has area:
OA'B'=r²*tan(π/n)

The total area for the circumscribed polygon then, will be given by UE=n*OA'B', so an upper bound for the area of the circle will be:
UE=n*r²*tan(π/n) (2)

Finally, LE < E < UE and (1),(2) give:

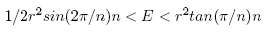(8)

Now, rewrite (8) as:

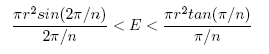(9)

and note that when n->∞, x=π/n->0, lim_x->0sin(2*x)/(2*x)=1, lim_x->0tan(x)/x=1, so by the squeeze limit theorem, (9) =>

Estimation of Perimeter:

Similarly the perimeter P of the circle can be calculated as follows:

AB as before, is:

AB=2*r*sin(π/n)

The total perimeter for the inscribed polygon then, will be given by LP=n*AB, so a lower bound for the perimeter of the circle will be:
LP=2*n*r*sin(π/n) (10)

A'B' is:
A'B'=2*r*tan(π/n)

The total perimeter for the circumscribed polygon then, will be given by UP=n*A'B', so an upper bound for the perimeter of the circle will be:
UP=2*n*r*tan(π/n) (11)

Finally, LP < P < UP and (10),(11) give:

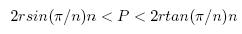(12)

Now, rewrite (12) as:

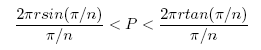(13)

and note that when n->∞, x=π/n->0, lim_x->0sin(x)/x=1 lim_x->0tan(x)/x=1, so by the squeeze limit theorem, (13) =>

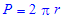
Here's then some Maple code based on the above method to estimate π:

> LE:=(n,r)->1/2*n*r^2*sin(2*Pi/n);
> UE:=(n,r)->n*r^2*tan(Pi/n);
> E:=r->Pi*r^2;
> evalf(LE(5000,1));
3.141591828
> evalf(E(1));
3.141592654
> evalf(UE(5000,1));
3.141593068

> LP:=(n,r)->2*n*r*sin(Pi/n);
> UP:=(n,r)->2*n*r*tan(Pi/n);
> P:=r->2*Pi*r;
> evalf(LP(500,1/2));
3.141592448
> evalf(P(1/2));
3.141592654
> evalf(UP(500,1/2));
3.141593068