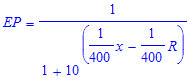One way to objectively judge the relative strength of game players is the ELO rating system. We will use a specific example to directly compare the relative strength of two players and thus deduce their Relative Mind Power.

The expected probability of winning for a player with rating R against a player with rating x, is:

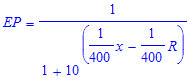(1)

Let's pick two specific examples then, with corresponding ratings 2500 and 1000:

> AR:=2500; #player A rating
> IR:=1000; #player B rating
> AEF:=x->(1+10^((x-AR)/400))^(-1); #expected probability of player with rating AR beating a player with rating x
> IEF:=x->(1+10^((x-IR)/400))^(-1); #expected probability of player with rating IR beating a player with rating x
> with(plots):
> plot(AEF(x),x=0..AR+1000,color=red);

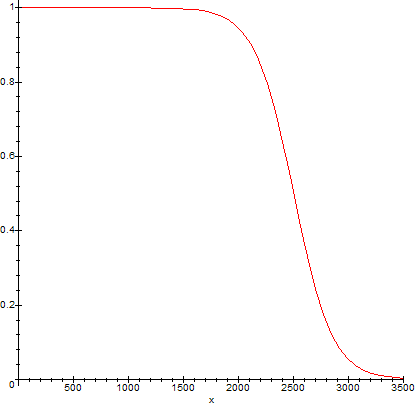
The function depicted above is a probability distribution. Hence a player with rating AR=2500 has a probability pA of winning a player with rating IR=1000:

> pA:=evalf(AEF(IR));#probability of player with rating AR=2500 beating a player with rating IR=1000
pA := .9998222036

while a player with rating IR=1000 has a probability pI of winning a player with rating AR=2500:

> pI:=evalf(IEF(AR));#probability of player with rating IR=1000 beating a player with rating AR=2500
pI := .1777963238e-3

Note that pA+pI=1.

Now let's follow an example of how the ratings are updated when the two players above play each other. A's rating is AR=2500, so according to FIDE, we use AK=10, and I's rating is 1000, so we use IK=15.

> NR:=proc(AR,IR,AS,IS)
>#Calculate new rating after a game
> local AE,IE,AK,IK,ARN,IRN;
> AK:=10;IK:=15;
> AE:=(1+10^((IR-AR)/400))^(-1);#expected A
> IE:=(1+10^((AR-IR)/400))^(-1);#expected I
> ARN:=AR+AK*(AS-AE);#new A
> IRN:=IR+IK*(IS-IE);#new I
> print(`ELO A`, evalf(ARN));
> print(`ELO I`,evalf(IRN));
> end:

The parameters now determine the outcome. There are three possible outcomes for the scores AS, IS:
AS=1 and IS=0, AS=1/2 and IS=1/2 and AS=0 and IS=1. Let's see the results:

>AS:=1;IS:=0;#stronger player A wins
>NR(AR,IR,AS,IS);
ELO A, 2500.001778
ELO I, 999.9973331

>AS:=1/2;IS:=1/2;#draw
>NR(AR,IR,AS,IS);
ELO A, 2495.001778
ELO I, 1007.497333

>AS:=0;IS:=1;#weaker player I wins
>NR(AR,IR,AS,IS);
ELO A, 2490.001778
ELO I, 1014.997333

We see that the only cases which really matter for I are the draw and win cases, because these are the cases which raise his rating and lower the rating of A.

Relative Mind Power in Chess

We can now define the Relative Mind Power (RMP) to be the ratio: pA/pI, or formally, for two players with ratings AR and IR, and AR>IR:

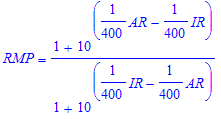
Using Maple to calculate:

> AR:=2500;IR:=1000;
> RMP:=(x,y)->AEF(x)/IEF(y);
> evalf(RMP(IR,AR));
5623.413252

In other words, the mind of a player with a rating AR=2500 is roughly 5623 times (!) more powerful than the mind of the player with a rating IR=1000. Now you understand why it is so difficult to beat stronger rated players.

You may ask, in what sense is A's mind more powerful than I's? In other words, how does this difference/ratio in power manifest? Exactly in the sense of influencing future events in chess in terms of statistics.

Let's see some examples: Suppose there are three people, A, I and O, an observer. Then if A's and I's ratings are the same, O can make the probabilistic prediction that I needs to play roughly 1 game(s) to see a draw. That's exactly what RMP is in this case.

When A and I have different ratings, say AR=2500 and IR=1000, the expected probabilities of winning are pA=.9998222036 and pI=1-pA, so O can make a fairly safe prediction that I needs to play roughly pA/pI=pA/(1-pA)=5623 games to win one. That's again RMP.

Now suppose A and I have the ratings AR=2400 and AI=2000. In this case, O can again make a fairly safe prediction that I must play roughly pA/(1-pA) games to win one. That's exactly RMP=10, in this case.