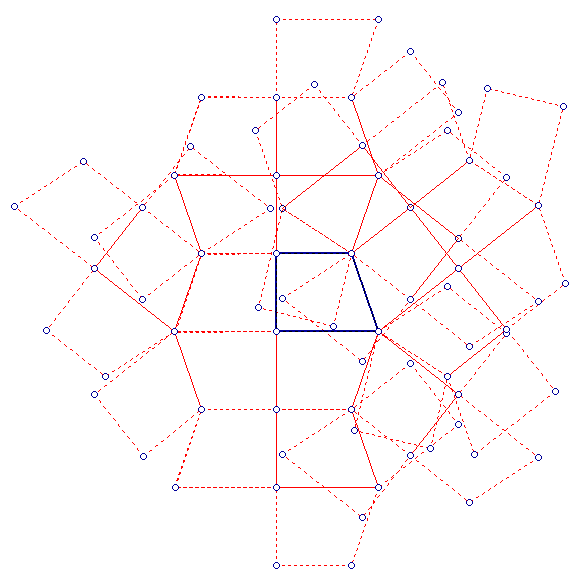
Fig. 1: Virtual image of room because of mirror AB
When you look at a mirror AB, a perfectly symmetric reflection of the entire room is created inside the mirror. This is equivalent to a virtual image of the room the mirror sits in, in the direction of the wall which holds the mirror, as in Fig. 1.

What happens if we place mirrors on all four walls of a room? Each mirror creates a virtual image of the room, in the direction of the wall which holds the mirror.
Further, because the virtual images contain images of the real mirrors, an infinity of virtual rooms is created, going infinitely deep into virtual land.
EucliDraw allows a dynamic visualization of such a situation, down to any desirable level. Fig. 2 shows the situation for a room in the shape of a trapezium with mirrors on all four walls and the virtual images of the room going up to level 2.
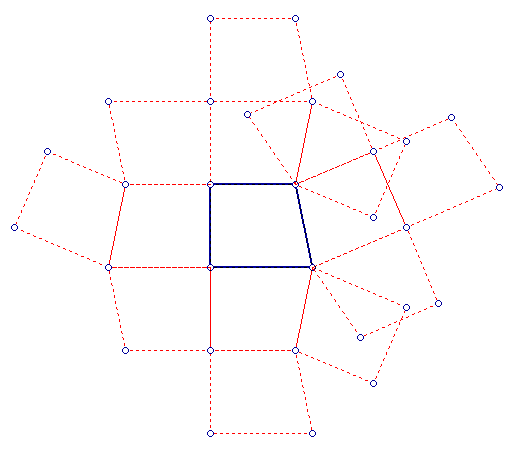
Fig. 3 is the same situation down to level 3, with the walls being parallel.
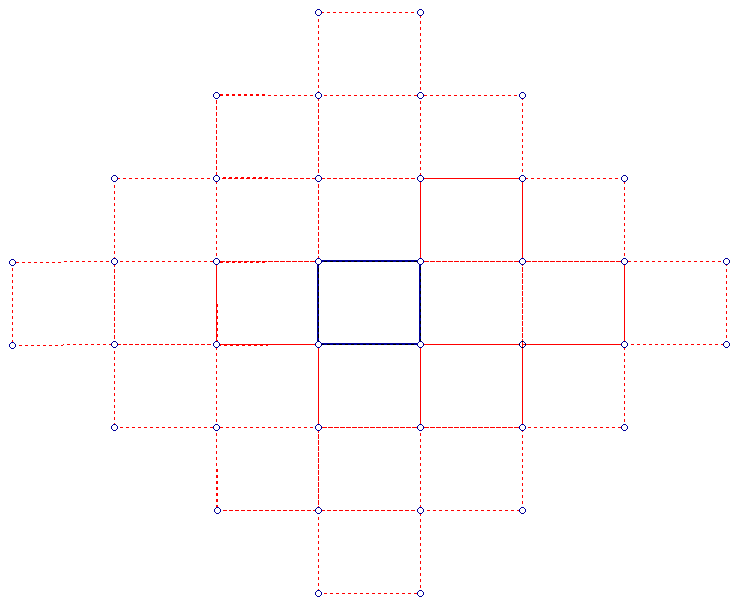
If the walls are non-parallel, the situation becomes quite complex and is very interesting, as in Fig 4: