Certain Maple tricks can be useful to sometimes see the "overall" behavior of specific functions, in order to gain some insight about how a function behaves at extreme points or to see how many roots it has.

On 20/1/2003 the author posted this question to the newsgroup sci.math. David W. Cantrell partially answered the question in 2007, with this post.

In essence we are looking for a transformation T that maps the graph of an arbitrary function into some finite interval, such as [-1,1]. If we call our function f(x), then translating David's Mathematica code to Maple, we get:

> f:=x->(some function of x);
> g:=x->x/(1-abs(x));
> ginv:=x->x/(1+abs(x));
> T:=x->ginv(f(g(x)));
> with(plots):

In other words, one such transform is T(x)=g^-1(f(g(x))), with g(x)=x/(1-|x|).

Let's see some examples of how the transform T matches Maple's built in overall graphing:

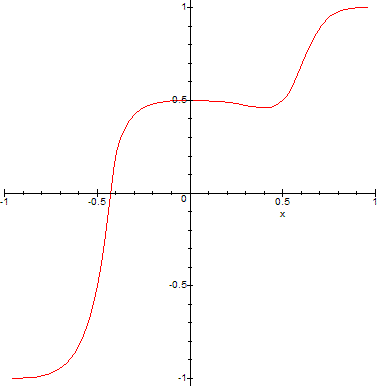
> f:=x->x^3-x^2+1;
> plot(T(x),x=-1..1); plot(f(x),x=-infinity..infinity);

     

Not bad. The transform looks very close to what Maple uses for its x=-infinity..infinity graph. A second example, shows that this transform can fail however:

> f:=x->x^12-2^x;
> plot(T(x),x=-1..1); plot(f(x),x=-infinity..infinity);

     

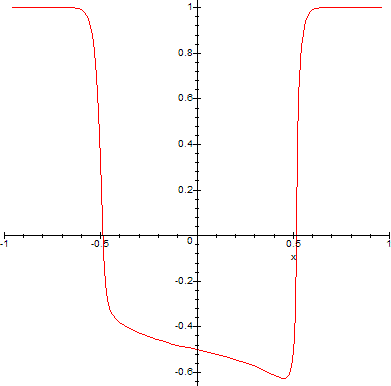
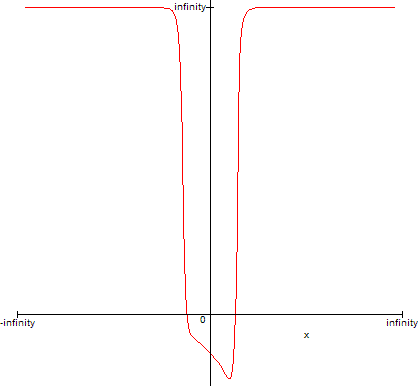
Both T and Maple V's internal transform fail, because f has three roots, given by: {-12*W(log(2)/12)/log(2), -12*W(-log(2)/12)/log(2),-12*W(-1,-1/12*log(2))/log(2)}, where W is the Lambert W function. Maple V misses the third root given by the non-principal branch of W. Maple 9 graphs it correctly:

     

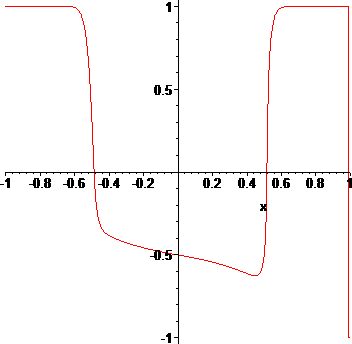
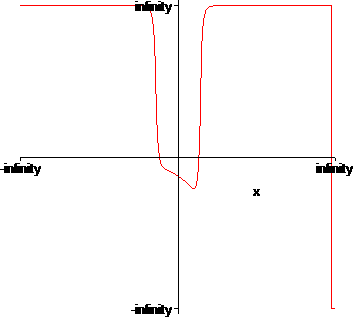
The fact that Maple 9 produces correct graphs, means that both the T transform and the internal transform Maple V uses for overall graphing are not handled correctly in version V, hence it's a bug.