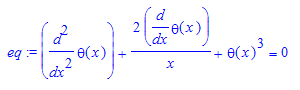
Lane-Emden equation for a n=3 Polytrope
Let's see if we can model the structure of the sun, using some interesting mathematics. We start by using the polytrope model [1], so we use Maple to get some interesting results. Let's load some parameters:
> restart;
> n:=3; #polytrope index for sun
> dc:=160000; #density at the core (kg/m3)
> Pc:=10^(16.53); #pressure at the core (Pascal)
> G:=6.67428*10^(-11); #gravitational constant (m3/kg/s2)
> r:=6.955*10^8; #radius of the sun (m)
> zeta:=r*(4*Pi*G*dc^2/(n+1)/Pc)^(1/2); #run extent for solution
> evalf(%);
Let's now build the fundamental differential equation for the model, the Lane-Emden equation [2/3]:
> eq:=diff(theta(x),x$2)+2/x*diff(theta(x),x)+theta(x)^n=0;
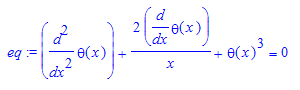
The equation cannot be solved analytically for n=3, so we solve it numerically:
> dsol:=dsolve({eq, theta(0)=1, D(theta)(0)=0},
theta(x),range=0..zeta,type=numeric,output=listprocedure);
> y:=eval(theta(x),dsol);
Now we calculate the density and pressure as a function of radius:
> d:=x->dc*y(x)^n; #density as a function of radius
> K:=Pc/dc^(1+1/n); #calculate constant K
> P:=x->K*d(x)^(1+1/n); #pressure as a function of radius
> rext:=fsolve(d(x)=0,x=0..zeta); #find where density drops to 0, in [0,zeta]
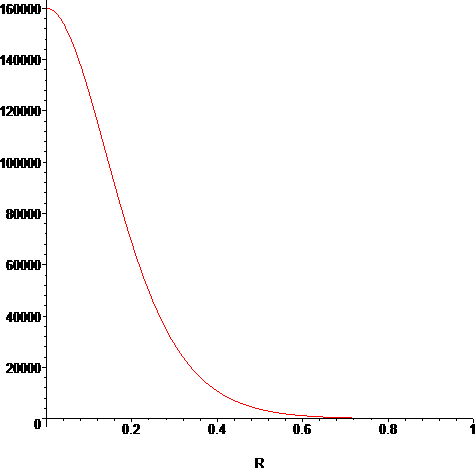
We now normalize the radius with respect to rext and what do we get?
> with(plots):
> plot(d(R*rext),R=0..1);
> plot(P(R*rext),R=0..1);
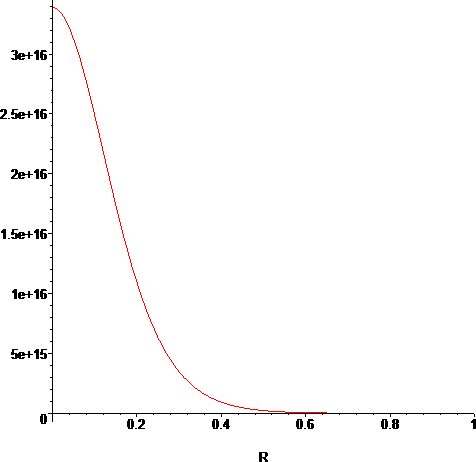
The first graph agrees fairly well with the data on the graph of Wikipedia's polytrope page [1], and with [4], [5] and [6], which give the density of the sun as a function of its radius.