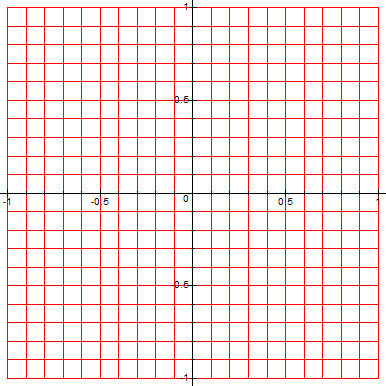
The following Maple code builds a 10x10 grid of the complex plane z:

> with(plots):
> f:=(rho,theta)->rho*exp(I*theta);
> nmax:=10; #subdivision for complex plane grid
> us:=z->z/nmax; #normalize to unit square grid
> w:=z->us(z); #function to be mapped into w-plane (here w=z=id)
> for n from -nmax to nmax do
> hor[n]:=complexplot(w(f(rho,0)+n*I),rho=-nmax..nmax,color=red); #horizontal lines
> od:
> h:={}:
> for n from -nmax to nmax do
> h:=h union {hor[n]};
> od:
> for n from -nmax to nmax do
> ver[n]:=complexplot(w(f(rho,Pi/2)+n),rho=-nmax..nmax,color=red); #vertical lines
> od:
> v:={}:
> for n from -nmax to nmax do
> v:=v union {ver[n]};
> od:
> grid:=h union v:
> display(grid);

Here's the resulting grid:

By interjecting a suitable function in the line, for example:

> w:=z->cos(us(z)); #function to be mapped into w-plane (in this case "cos"),
we can visualize how the function transforms the z-plane to w-plane. Here are some examples of running the above code with different complex functions^[1][2]:

sin(z)

cos(z)

z²

z^1/2

exp(z)

log(z)

z*exp(z)

Lambert's W(z) function

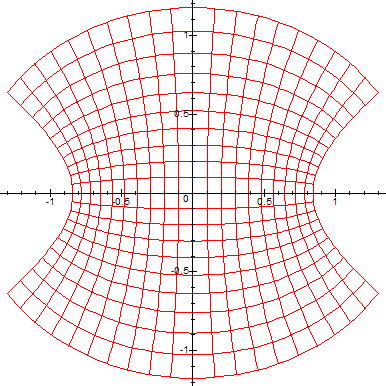
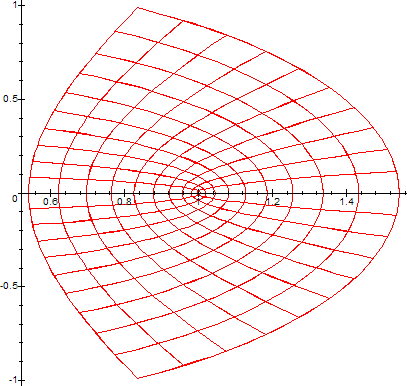
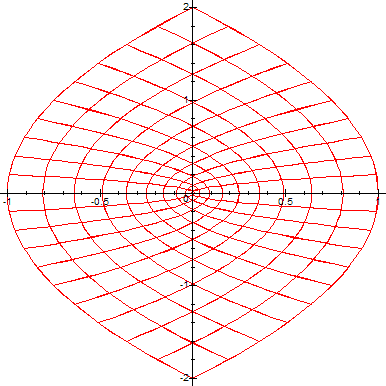
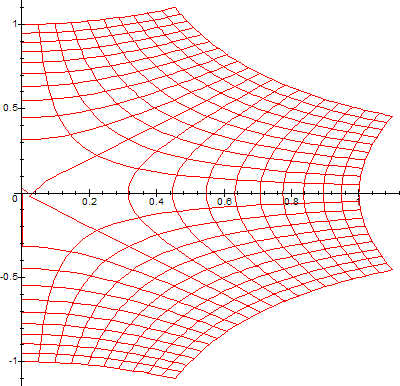
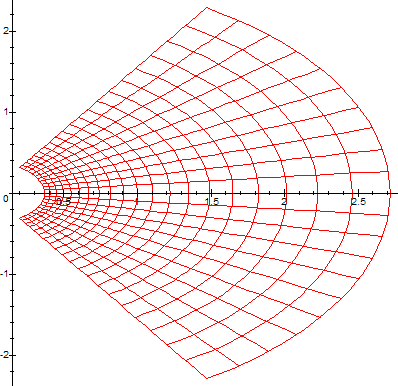
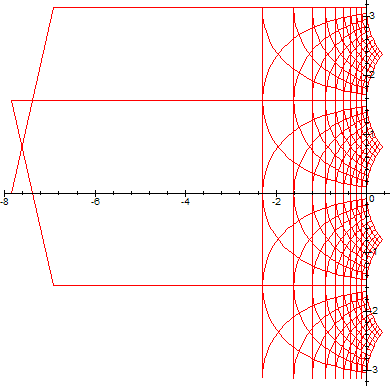
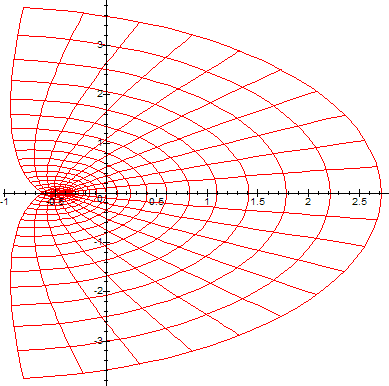
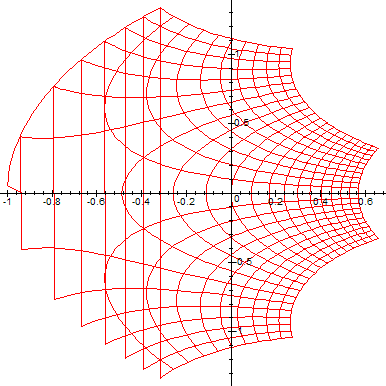
(Note that the range of W is delimited on the left by the curve -y*cot(y)+y*I. For more details on this, consult this article).

Notes

1. Compare with David Bau's Conformal Map Viewer.
2. For some Maple 18 code that implements color conformal mapping as above, consult Maple Primes, at: Conformal Code Viewer.