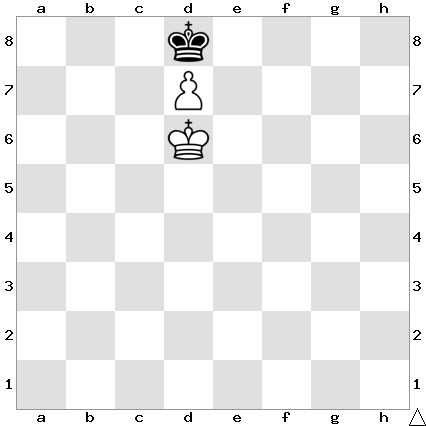
Encoding value:17543043497050476099565
Estimated time to reach this configuration on this machine: 1.370112e+16 secs = 4.344598e+08 years
This page is based on the idea of Every Icon Project, © John F. Simon. This reference was given to the author by Johan E. Mebius, so the author's thanks go to him.
The legal chessboard configurations are bounded above by all chessboard configurations t (legal & illegal). A simple counting argument shows that t = 1364, since we have the 6 possible values for a piece (P,N,B,R,Q,K), 2 possible colors for a piece (B,W) and an empty square. We have a total of 64 squares, so the total number of configurations is (2*6+1)64=1364[1].
We next choose an encoding for the chessboard configuration. The most natural choice is the chessboard being a base-13 word of maximum length 64. So we set empty=0, bP=1, wP=2, bN=3, wN=4, bB=5, wB=6, bR=7, wR=8, bQ=9, wQ=10, bK=11, wK=12.
If we now write a simple program which runs from 0 to t-1, the program will eventually display all chessboard configurations, hence necessarily all legal configurations as well.
The program will start with an empty board and end with a board full of white Kings and then the cycle will repeat. Before it repeats, it will pass through every possible legal chess configuration, which means that it will eventually display all chessboard positions of every possible game, including not only all the games that were ever played, but also all the games that will ever be played.
Obviously you won't live long enough to see most interesting configurations appear (the entire human race or even the universe may be extinct by then), so it's easier to just bench-mark your machine so you can input a specific configuration and see how long it will take for this configuration to appear on your machine and with your version of Maple.
Download a Maple 9 worksheet that does all this benchmarking automatically, after you input a configuration.
Here are the timing results for some chessboard positions on the author's machine[2].



