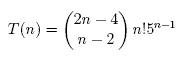
A very popular game, which also aired on some British tv show, was to target and hit a specific number, given three numbers which could be added, subtracted, multiplied, divided or exponentiated. For example:
Suppose you are given the numbers n1=3, n2=9 and n3=12. Can you determine if a suitable operational combination of n1,n2 and n3 can produce the number n=324 using only {+,-,*,/,^}?
By hand this is a difficult game and it is a useful mental exercise for students. Let's write a Maple program which calculates this automatically. The key procedure is PF, which basically implements the code on Expression Evaluation Using a Stack[1]:
> restart;
> with(combinat):
> PF:=proc(L)
> local s,e,x,y,r1,r2,r;
> s:= stack[new]();
> for e in L do
> if type(e,procedure) then
> r1:=stack[pop](s);
> r2:=stack[pop](s);
> r:=evalf(e(r1,r2));
> stack[push](r,s);
> else stack[push](e,s);
> fi;
> od;
> r:=stack[pop](s);
> if stack[empty](s) then
> r;
> else
> -1;
> fi;
> end:
Next, let's input three numbers and a target:
> n1:= 3; n2:= 9; n3:= 12; n:= 324;
> A:= permute([n1,n2,n3]);
> ops:= [`+`,`-`,`*`,`/`,`^`]:
> B:= [seq(seq([a,b],a=ops),b=ops)]:
> R:=
[seq(seq([a[1],a[2],a[3],b[1],b[2]],a=A),b=B),seq(seq([a[1],a[2],b[1],a[3],b[2]],a=A),b=B)]:
The above permutes the postfix expressions obtained by n1,n2 and n3 using 2 operators.
Let's now define the function which minimizes the distance from the target.
> FM:=proc(n,L)
> local i,m,nm,len;
> len:=nops(L);
> m:=infinity;
> for i from 1 to len do
> nm:=E(L[i]);
> if nm
> m:=nm;
> print(m,L[i]);
> fi;
> od;
> end:
Finally let's call it on this specific example:
> FM(n,R);
300., [3, 9, 12, +, +]
213., [3, 9, 12, *, +]
189., [9, 3, 12, +, *]
180., [12, 3, 9, +, *]
0., [3, 9, 12, *, *]
Success! The first column shows the distance to target and the postfix expression following is the one which gives this result. The last example hits n exactly, since the distance is 0. In other words, 324=9*12*3.
Try a different example:
> n1:= 2; n2:= 22; n3:= 159; n:= 1224;
> FM(n,R);
1041., [2, 22, 159, +, +]
884., [22, 2, 159, *, +]
581., [159, 2, 22, ^, +]
525.000000, [22, 2, 159, /, *]
74.863636, [22, 2, 159, ^, /]
In the last example above, there is no success and the closest we can come to 1224 with the numbers given is 159^2/22.
Based on the procedure above, we can calculate the cardinality of the enumeration of the possible postfix expressions for the general case of n operands and n-1 operators, with the 5 operators being: [+,-,*,/,^]. Let the general expression be:
E=[x,x,|y,y,y,...,y,|z]
The list size is always |L|=n+n-1=2*n-1. The first two positions [x,x] are always occupied by operands, since by definition the operators are binary. The last position [z] is also always an operator, because of the same reason. There are then 2*n-1-3 remaining slots, in which we need to distribute the remaining operators and operands.
Ignoring the commutativity of the two ops +,*, and assuming ni=/=nj for all pairs of operands, the total number of postfix expressions to be checked will be:
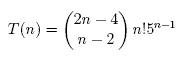
Check with Maple:
> T(3)# 3 operands 2 operators:
300
> nops(R);
300