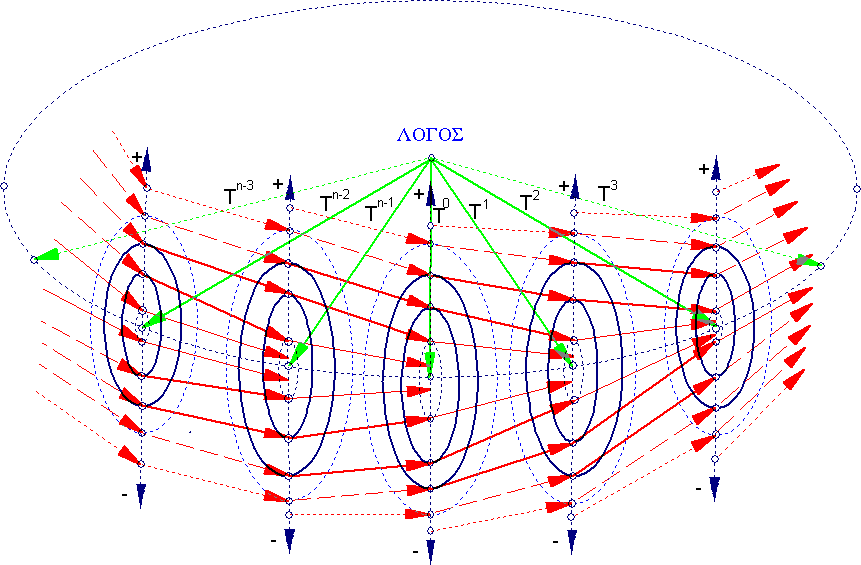

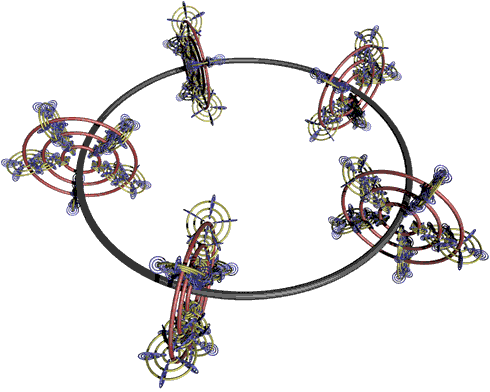
A view of how this author imagines the Universe. This is a cross-section of a toroid
manifold fractal. Universes and sub-universes are indicated by ellipses.
The First Cause[1] at the
center of the toroid structure, generates/sustains the subuniverses, in a round robin
fashion. The subuniverse generation is indexed as T0 through
Tn-1, n in N, and each ray sustains m concentric subuniverses, indexed as
Tkm, m in N. At Tk0, there is a copy of the
First Cause (as a rotationally fixed point of f, see below), which generates
subuniverses at lower levels.
The subuniverses fold within each other through a contractive homeomorphism f, indicated by the red arrows, creating a "time/reality funnel" or "time/reality sheet", consisting of a continuous stream of quaternion "events" (t,x(t),y(t),z(t)) for an individual mind, giving the impression of continuous consciousness.
f wraps back on itself around the main toroid structure and the only points that
survive are the rotationally fixed points of f , for each Tkm.
Following for example the manifold sheet of any one subuniverse
Tkm through f, as
Tkm->f(Tkm)->f(f(Tkm))->...,
k, m in N, one can get a representation of what's happening in 3D, topologically. The
red ellipse is universe Tkm. The only point that survives, the
"last" fixed point of f, a copy of the First Cause, re-creates subuniverse
Tkm, or jumps to a different/unknown subuniverse
Txy. At that point, there is an "explosion", as that's the only
point in time when f is not contractive.
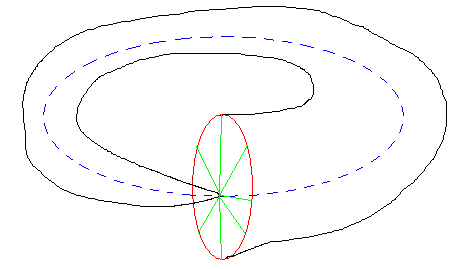
The reality funnel considered thus, bares an interesting connection with the notion of Ouroboros.
Inside every Tkm lies the universe Tkm-1, which generates (through f) a similar manifold which wraps back on itself. Outside every Tkm lies the universe Tkm+1, which also wraps back on itself. In effect, the only points that pass through all universes are the fixed points of f, indicated by the dotted blue ellipse.
Accordingly, the main toroid structure, T, in 3D, looks like the shape above, although in the figure each such structure is represented by an ellipse (the fixed points of f). The toroid sheets here separate space into "inside" and "outside". At the moment of Tkm 's "birth", there is no such differentiation.
Each subuniverse Tkm is a replica of the main toroid structure
T. That means that the centers of Tkm, k,m in N generate p
creative rays, indexed as Tkmp, k,m,p in N, exactly
like the main torus generates n rays, n in N. Each ray
Tkmp, p in N generates q subsubuniverses, indexed as
Tkmpq, k,m,p,q in N, and for each of those
a similar contractive homeomorphism wraps each sheet
Tkmpq onto itself, similarly to the way f
acts on the subuniverses Tkm, k,m in N.
The process continues, and at level r, we are indexing the sub...subuniverse as Tkmpq...rs, k,m,p,q,...,r,s in N, which is self-similar to the original toroid structure T. The green vectors are the "First Cause", fixed point "sustainers" of the individual subuniverses, branching down all the way to non-existence.
Time moves up with the main toroid structure, pointed to by the vertical axes with the + signs and right for all subuniverses in what physicists call "right handed way". This means that the main toroid structure moves in time upwards and the first order subuniverses to the right. Time does not exist while the "First Cause" "switches" its attention from subuniverse Tk to subuniverse Tk+1. When this happens, the entire structure falls into "suspended animation" for an infinitesimal time increment dt. dt is of the order of Plank scale time 10-28 to 10-34 seconds, yet the "First Cause" can "stay" within universe Tk as long as it wants.
In this structure, n denotes the number of first order subuniverse divisions applied recursively to the base circle. The recursive depth to which those divisions are applied is denoted as d. Concentric subuniverses are indexed by m. Accordingly, approximations of the structure are denoted as T(n,m,d).
Here is a .gif animation of the toroid structure T(6,1,4) done in Maple by C W of comp.soft-sys.math.maple.

Here are some videos of high quality animations done by C W:
Here is a static picture of the toroid structure T(6,1,4) done by Paul Burke using POVRay.
For more static pictures for different values of n and d, see Paul Burke's directory, here. The pictures in his page (from top to bottom and left to right) are: T(6,1,4), T(10,1,3), T(10,1,4), T(5,1,3), T(5,1,4), T(18,1,4) and T(n,1,4) for some large n.
Here is a static picture of the toroid structure T(5,3,4) (which is closer to the structure in the first figure) done by Paul Burke again using POVRay.
In a sense the First Cause is akin to the the operating system or the time engine for the toroid structure. The author don't know if the structure continues to an infinite sub-level or to an infinite super-level. Doing so, would require infinite speed for the "First Cause" to sustain all subuniverses properly. In other words, if the structure was T(n,m,∞) the author is not exactly sure how the "First Cause" can "cover" all the subuniverses in a finite time.
Although T(n,m,∞) sounds like a bit much, the main structure may generate many
super-universes similar to itself, by wrapping back on its past, creating a super
toroid fractal manifold one level up from what you see in the first figure. The new
super-universe has the same properties as the original figure and this process may
continue upwards and to the right, each time "time" being folded upon itself, in the
direction of the homeomorphism arrows.
Imagine this immense toroid manifold folding out and folding back in. When it folds out, it creates super-universes and subuniverses both upwards and downwards to any finite super-level or sub-level. When it folds back in, it destroys super-universes and sub-universes.
Alternatively, the entire structure can be seen as a fractal toroid solenoid, where from the main torus emanate n rays, each generating m concentric toruses, normal to the main torus' circle as in figure 1. Then each of those toruses has the same structure as the main torus T and additionally each torus is mapped through a contraction to a torus to its right. The process continues to any level, either downwards (generating smaller toruses) or upwards, generating super-toruses by having the main torus wrapping against itself, any number of times[2].
Most people seem to think that what astronomers call "the Universe", is an a-personal vast structure, independent of perception and consciousness. Whenever this author writes about any "universe", it is understood that he means "the observable universe", in other words a "universe" which is explicitly associated with a specific observer's five senses, his vision notwithstanding. This author fails to understand what a "universe" independent of human perception and consciousness is. Such a universe (apparently) seems to exist only as a mental structure in the minds of scientists and may or may not have a tangible existence, since it cannot be surveyed in its entirety and since when consciousness disappears it goes too[3]. To illustrate "the observable universe", we return to the picture of the "time/reality-funnel" which was presented above:

The above "funnel" is basically a discrete stream of "events" in space-time. We notate a single such event as a quadruple E(t)=(t,x(t),y(t),z(t)) = t+v(t). t then is the scalar part of the event and v(t) is the vector part of the event. The event t+v(t) is a point in space-time.
The observer's coordinate system is the birth-point relative to some major event in time. Modern historians choose the birth of Jesus as the time reference for events in history, therefore the observer's birth (as an event in time) gives rise to a unique time coordinate tb(irth) and a unique space coordinate v(tb).
The time coordinate tb is measured relative to 0AD and the space coordinate v(tb) is measured relative to Jesus' place of birth. For example, the author was born in September 2, 1964, so tb=02/09/1964 in years. He was born in Athens, Greece, so v(tb)=(x(tb),y(tb),z(tb)), the coordinates of Athens relative to Bethlehem in Cartesian coordinates.
Since most of us measure space-time relative to our birth, we switch reference frames by transferring the origin to the above point by applying the transformations:
tb*=t-tb
v(tb)*=v(t)-v(tb)
Therefore the observer's new reference system will be transformed to tb*=0 and v(tb)*=(0,0,0). This is the event of the observer's birth, which the observer now will use as the new origin (0,0,0,0). The observer now starts measuring "reality" (time and space) always relative to this new origin.
"Reality" is delimited by the full spatial extent of the vector part of the observer's life at time t, R(v(t)). When the observer is a newborn, R(v(t)) is small. As the observer grows and consciousness gets organized, R(v(t)) increases. That's why the "time/reality funnel" starts being close to a singularity. R(v(t)) on a newborn observer is shown with red ellipses as the observer grows.
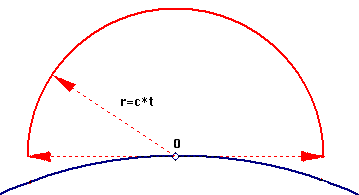
R(v(t)) is always bounded by the fastest communicator of information in any universe: Light. Therefore, at time t, the observer's "light-sphere", is defined as:
L(t)={(x(t),y(t),z(t)) in R3: x(t)2+y(t)2+z(t)2 = (c*t)2} (1)
The observer's "reality" R(v(t)) then, must be the set of all points in R3, which are always bounded by the light-sphere L(t), that is the set of points which are at a distance of less than c*t from the observer:
R(v(t))={(x(t),y(t),z(t)) in R3: x(t)2+y(t)2+z(t)2 < (c*t)2} (2)
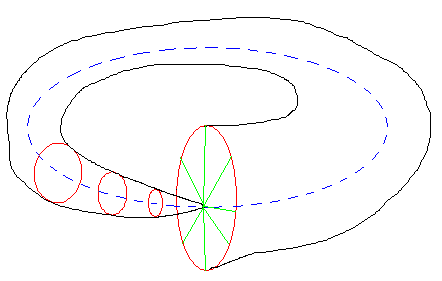
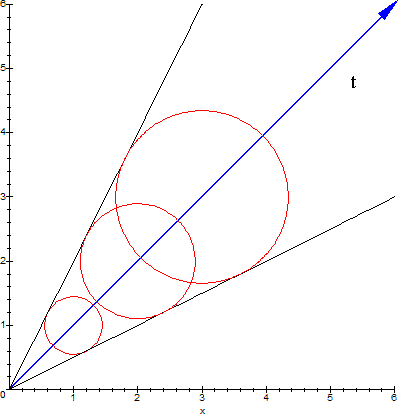
We now unfold the toroid time/reality funnel of the observer's events relative to time, which is linear. Here is a 2D representation. L(t) is denoted by the red circles and it always rides on the vector of time, t.
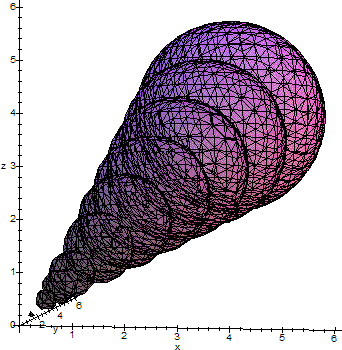
Here's the situation as it happens in 3D. The observer's "reality" R(v(t)) is delimited by the individual spheres L(t), which have radius c*t. As time t passes L(t) (and thus R(v(t))) grows. L(t) is the observer's event horizon.
Definitions (1) and (2) above of the light-sphere L(t) then naturally define a distance differential (ds) in space-time:
ds2=dx(t)2+dy(t)2+dz(t)2-c2*dt2
ds above then agrees with the definition of the Minkowski metric in Special Relativity. The null geodesics therefore are described by the equation:
dx(t)2+dy(t)2+dz(t)2=c2*dt2.
These are the light-spheres L(t) of radius c*t shown above which "ride" on time and which lie along the four dimensional light-cones described by the birth itself, in both figures above.
At any given time t, any information from objects outside the observer's event horizon L(t) (that is at distances greater than c*t), hasn't reached the observer yet, therefore any event outside the light-cone of the observer is not causally connected with the observer.
The birth of an observer takes place when two independent observers A and B mate and produce a new observer as follows:
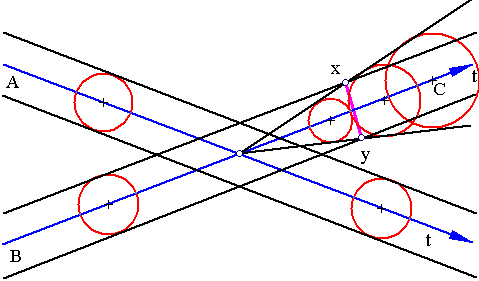
Observer B is the female, A is the male. They synchronize their time vectors and unite. The offspring, observer C, starts surveying his/her mother's reality first. As he/she grows, observer C surveys larger and larger parts of his/her mother's reality, until his/her reality C bursts out of the reality of B. This is the moment of birth at x and y. All this of course happens in three dimensions.
Although time is thought of as continuous, in reality it is discrete with points spaced apart on the time vector every 10-28 seconds: Plank's time scale = Δt. As such, the difference between any two centers of the spheres above is at least Δt and this creates the illusion of time continuity. In effect, Δt is the "minimum resolution" of The First Cause's Consciousness or the "program" that directs the evolution of all the individual time-reality funnels. In the above two images, the minimum time difference between circles/spheres is a multiple of Δt to allow the respective R(v(t))'s to be visualized as separate. In reality the centers of the R(v(t))'s are Δt apart.
This "growth" of L(t) (and thus of R(v(t))) is as if the observer's consciousness is "sampling" reality at least at the rate of dr/dt=d(c*t)/dt=c or 3*10-20 meters per Δt. Objects outside L(t) eventually fall into L(t) after sufficient time elapses. The notion of "now" therefore does not exist, because any information that is being communicated to the observer from reality, has taken some time to reach him. Even information from an object 1cm away from an observer, takes 1/3*10-10 seconds to reach the observer.
R(v(t)) is a full sphere only when the observer stands in empty space and looks at a night-sky or at the sky above the atmosphere. For an observer standing on earth, R(v(t)) takes various shapes depending on where his vision is focused and how it is used. Standing on Earth and looking at the night-sky for example, R(v(t)) looks like a hemisphere:
In the above case the viewer is looking at events E(t), d meters away, where d2=x(t)2+y(t)2+z(t)2 and d/c seconds in the past.
Ideally then, consciousness is a mental sphere which always rides on time t. This sphere shrinks and expands depending on how the observer uses his faculties (mainly his vision). Therefore R(v(t)) can vary for example from the dimensions of a room with 8 walls (for an observer inside a closed room), to a sphere with radius c*t. This is the "time-reality funnel" described on the corresponding figures.
When the observer stands still between two moments in time t1 and t2, then x(t1)=x(t2), y(t1)=y(t2) and z(t1)=z(t2), so the vector parts of the two events E(t1) and E(t2) are identical: v(t1)=v(t2), even though the scalar parts are not equal: t1=/=t2.
When the observer moves spatially between two moments in time t1 and t2, then at least one of the following holds: x(t1)=/=x(t2), y(t1)=/=y(t2) and z(t1)=/=z(t2), so the vector parts of the two events E(t1) and E(t2) are different: v(t1)=/=v(t2).
Since time always moves forward, consciousness also moves forward. There's no way to jump from an event in time E(t1) to an event in time E(t2) with t2-t1 > Δt, unless either the observer undergoes general anesthesia or goes to sleep. In this case the time vector is interrupted and made discontinuous and as a result the R(v(t))'s are also made discontinuous, since they ride on time. For anesthesia and sleep, the situation is depicted in the following figure:
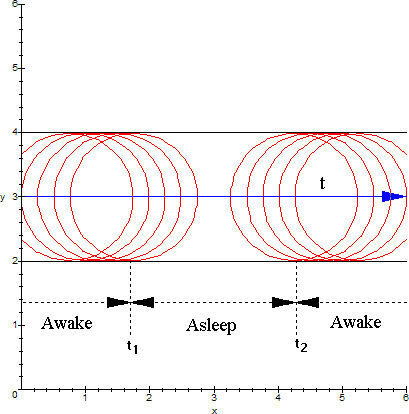
Sleep differs from general anesthesia in that during sleep there is partial awareness, although this awareness is unrelated to reality, while during anesthesia there's absolutely no consciousness. In the above figure, while t1 < t < t2 consciousness shuts down, so R(v(t)) has no meaning. Consciousness and thus R(v(t)) resume after t2.
The observer births of figures 8-10, create the notion of "chained-births" in the toroid-universe, because every observer has a female parent. Therefore there exists a chain of universes/realities with each one being (initially) inside another one (that of his/her parent. Inside every Tkm lies the universe Tkm-1, which generates (through f) a similar manifold which wraps back on itself. Outside every Tkm lies the universe Tkm+1, which also wraps back on itself).

The maximum observable universe then, seems to be the reality of the left-supremum of the above chain births. In other words, the maximum observable universe as this author understands it, seems to be the reality of the first "observer". Whether this "observer" was a man or something else, the author does not know. This "reality" has still radius c*t0, but now t0 is of the order of millions of years. This observer has managed to survey the largest part of reality so far and we, as observers down the chained-sequence of births/light-cones, are surveying what he surveyed, asymptotically[4][6].
The reality of this observer then, R(v(t0)) is a 3-dimensional sphere of maximum radius c*t0 light-years, a virtual spaceship in time and space, within which all of us move and live. His corresponding light-sphere, L(t0) is the boundary between existence and non-existence. Although for each one of us L(t) is contained in some other universe, the first observer's light-sphere L(t0) and corresponding light-cone are the upper bound for any observable universe.