The tetraroot or hyperroot^[1] of order n of x, ^1/nx is defined by the rule:

^1/nx=y <=> x=ⁿy, or equivalently: ⁿ(^1/nx)=^1/n(ⁿx)=x.

There appears to be a process based on continued fraction decomposition which allows the reduction of any rational hyperexponent in tetration to a tetraroot hyperexponent (a unit fraction). The process for the interval (0,1) can be summarized as follows:

Given m/n with GCD(m,n)=1 and 0<m/n<1:

1. mirror m/n into n/m using the definition of tetraroot.
2. use definition of tetration until the resultant hyperexponent falls inside (0,1).
3. repeat 1) and 2) until all tetration hyperexponents are unit fractions.

Let's see an example:

What is ^7/11e? Call it a₁. Then, applying the algorithm above:

^7/11e=a₁=>
e=^11/7a₁ (mirror)=>
e=a₁^(4/7a₁) (use definition)

Now we are looking for ^4/7a₁:

^4/7a₁=a₂=>
a₁=^7/4a₂ (mirror)=>
a₁=a₂^(3/4a₂) (use definition)

Now we are looking for ^3/4a₂:

^3/4a₂=a₃=>
a₂=^4/3a₃ (mirror)=>
a₂=a₃^(1/3a₃) (use definition)

We now back substitute everything, to obtain:

e=a₁^a₂=>
e=(a₂^(3/4a₂))^a₂=>
e=(a₂^a₃)^a₂=>
e=((a₃^(1/3a₃))^a₃)^{(a₃(1/3a₃))}

Now we only need solve the last equation for a₃. Solving with Maple, we get: a₃=1.418200508

We remember that we are looking for a₁, and using again back substitution, we get:

a₁=a₂^a₃=>
a₁=(a₃^(1/3a₃))^a₃

Substituting a₃=1.418200508 into the above, we get:
a₁=1.892317939 =>

^7/11e=a₁=1.892317939.

The algorithm 1-3 can easily be seen to be equivalent to the Maple code:

> reduce:=proc(m,n)
> local T,M,N;
> M:=m;N:=n;
> print(M,N);
> while M>1 and M<>N do
> T:=M;M:=N;N:=T;#flip
> print(M,N);
> M:=M mod N;#reduce
> print(M,N);
> od;
> end:

In the above example, the reduction was:

> reduce(7,11);

7, 11
11, 7
4, 7
7, 4
3, 4
4, 3
1, 3

It is easy to see that for any fraction m/n, with GCD(m,n)=1 and m/n<1, this algorithm always terminates on a unit fraction, hence tetrating to any rational can be expressed in terms of tetrating with tetraroots.

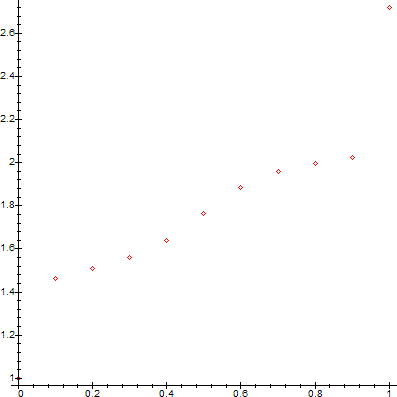
Let us see what happens with all the rational numbers m/10, m in {0,1,...,10}. Calculating the corresponding values for m/10, we find:

• ^0/10e=1
• ^1/10e=1.463958247
• ^2/10e=^1/5e=1.509672003
• ^3/10e=1.560286647
• ^4/10e=^2/5e=1.641090369
• ^5/10e=^1/2e=1.763222834
• ^6/10e=^3/5e=1.884498279
• ^7/10e=1.957858227
• ^8/10e=^4/5e=1.996820345
• ^9/10e=2.022406784
• ^10/10e=e=2.718281828

Plotting the values:

The function appears^[2] to be monotone increasing (although this is no actual proof). Although it looks discontinuous at 0 and 1, no statements can be made about its monotonicity, continuity, differentiability on (n,n+1), for Narural n including 0.

Notes

1. For more details on tetraroots, consult the article A Detailed Look at the Hyperroot Functions Using Lambert's W Function.
2. The function looks suspiciously similar to the function which Gus Weisman plots in his Mathematics page. Because Gus has a graph of a plot of the tetrate decomposition function in his next section and this graph is identical to the tetration timing graph which this author found when he executed the tetration algorithm presented here, the author tends to believe that Gus is using the same algorithm, although the author is not sure.