Determining the Zoom Magnification of a Video Camera

Version 1.0 of 10/2/2011-12:00 p.m.

Samsung HMX-H100 video cam
Samsung HMX-H100 video cam

Let's do some tinkering with Maple to see how high the HMX-H100 Samsung Video Camera can zoom optically.

The camera has a side-ways working Zoom switch, whose range is n=23 clicks. To determine the true range of the zoom, we need to photograph a distant image and apply the zoom to see how it affects the initial image. For this, we photograph a distant light source, using all zoom switches and we get a list of photos.

switch 1 cam magnification switch 2 cam magnification switch 3 cam magnification switch 4 cam magnification
switch 5 cam magnification switch 6 cam magnification switch 7 cam magnification switch 8 cam magnification
switch 9 cam magnification switch 10 cam magnification switch 11 cam magnification switch 12 cam magnification
switch 13 cam magnification switch 14 cam magnification switch 15 cam magnification switch 16 cam magnification
switch 17 cam magnification switch 18 cam magnification switch 19 cam magnification switch 20 cam magnification
switch 21 cam magnification switch 22 cam magnification switch 23 cam magnification switch 24 cam magnification

We now extract the dimensions of the photos in pixels using Photoshop. For each normally sized[1] cam photo above:

  1. Select the Magic-wand tool.
  2. Click inside the street lamp (white area) to determine the full extent of the street lamp.
  3. Select "Copy".
  4. Select "New..." to read the dimensions of the copied object in horizontal and vertical pixels.

After the above has been done for all photos, we remove all duplicates and we get a list of dimensions (x,y), which we input on Maple:

> restart;
> with(plots):
> PL:=[[17,11],[17,12],[17,12],[20,11],[22,13],[24,14], [26,13],[30,15],[35,17],[40,19],[47,21],[62,27], [83,33],[103,41],[122,47],[158,58],[208,78],[231,84], [253,92],[271,98],[338,120],[356,128],[430,156]]:

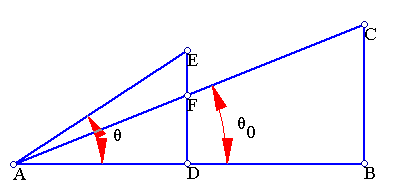
For an optical instrument and an object subtending an angle θ0 under magnification 1X and θ under magnification MX, the magnification M is defined as:

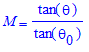
Magnification for optical instrument

The situation is depicted in the following diagram.

definition of magnification
Magnification for optical instrument: M=DE/DF

From the list of pixel sizes PL, we determine the average magnification with Maple:

> M:=array(1..nops(PL),[]);
> for n from 1 to nops(PL) do
> M[n]:=evalf(abs(PL[n,1]/PL[1,1]+PL[n,2]/PL[1,2])/2);
> od:

The luminaire lies at a distance of AB~30m, and has a size BC~35cm, therefore at magnification 1X, it subtends an angle θ0, such that tan(θ0)=BC/AB. With Maple,

theta0:=evalf(solve(tan(x)=0.35/30,x));#actual object angle @M=1.

Next, let us determine the angles the object subtends to, under different magnifications:

> theta:=array(1..nops(PL),[]);
> for n from 1 to nops(PL) do
> theta[n]:=solve(M[n]=tan(x)/tan(theta0),x);
> od;

Because the angles are small, tan(θn)/tan(θ0)~θn/θ0, so let's verify that we got the correct magnifications for all switches n\in {1,2,...,23}, using both calculations:

> for n from 1 to nops(PL) do
> print(n,evalf(theta[n]/theta0),evalf(tan(theta[n])/tan(theta0)));
> od;

1, 1.000000000, 1.000000000
2, 1.045450136, 1.045454545
3, 1.045450136, 1.045454545
4, 1.088226198, 1.088235295
5, 1.237938006, 1.237967914
6, 1.342197180, 1.342245989
7, 1.355563460, 1.355614973
8, 1.564068485, 1.564171123
9, 1.801955312, 1.802139037
10, 2.039814383, 2.040106952
11, 2.336425632, 2.336898395
12, 3.049653178, 3.050802139
13, 3.938581196, 3.941176471
14, 4.887965156, 4.893048128
15, 5.716369443, 5.724598930
16, 7.266297789, 7.283422460
17, 9.622909978, 9.663101612
18, 10.55904667, 10.61229947
19, 11.55305416, 11.62299465
20, 12.33974328, 12.42513369
21, 15.23397941, 15.39572193
22, 16.09756070, 16.28877006
23, 19.40066154, 19.73796791

If we instead used only lateral magnification[2], we'd get:

> for n from 1 to nops(PL) do
> print(n,M[n]);
> od:

1, 1.
2, 1.
3, 1.
4, 1.176470588
5, 1.294117647
6, 1.411764706
7, 1.529411765
8, 1.764705882
9, 2.058823529
10, 2.352941176
11, 2.764705882
12, 3.647058824
13, 4.882352941
14, 6.058823529
15, 7.176470588
16, 9.294117647
17, 12.23529412
18, 13.58823529
19, 14.88235294
20, 15.94117647
21, 19.88235294
22, 20.94117647
23, 25.29411765

Conclusions

For optical magnifications, the camera has n=23 zoom switches with maximum magnification achieved being M~24X on (x) (lateral), and maximum average magnification M~19.7X on (x,y) (lateral/longitudal)[3].

Notes

  1. The images on the table above have been reduced to 25% to save bandwidth. When measuring dimensions, one has to use the original-sized images.
  2. For lateral only magnification (x), we should recalculate with > M[n]:=evalf(abs(PL[n,1]/PL[1,1])); in the first Maple code loop.
  3. The camera can actually go higher, if one engages its Intelli-Zoom digital magnification. For this case, a similar measurement should be performed.