

In Hinduism and Buddhism in the heaven of Indra, there is a vast net or web of silken strands which spans across space infinitely in every direction. Every intersection hosts a shining luminous pearl. The surface of every pearl completely reflects every other, and the net as a whole. Likewise, each reflected pearl in itself reflects every other, with the process continuing ad infinitum. Indra's Net is alternatively known as Indra's Pearls or the Jewel Net of Indra.
It is said that the pearls themselves represent the souls of animated life. Within each such pearl, there is a virtually infinite universe of images - experiences, since all souls are connected. The whole network is illuminated by a single light source, metaphorically The First Cause.
Indra's Net may be taken as a philosophical allegory for various concepts, from the broad interconnected nature of the known universe, to more specific ideas such as self-similarity, or computer and neural networks.

Here the author renders depictions of sections of Indra's Net, using the ray-tracing program POVRay.
POVRay uses a (x,y,z) Cartesian system, with x being the horizontal axis with positive to the right, y being the vertical axis with positive up and z being the third axis going in and out of the computer screen, with positive pointing towards the computer screen.
In Indra's Net all the nodes (k,l,m) with k,l,m in Z are occupied by pearls, however such a situation cannot be reasonably rendered even with POVRay, because the number of reflections tends to infinity and the scene becomes saturated with light of constant luminosity.
On the rendering above and on the following videos, the author placed mirrored pearls of radius r=π/20 at (k,l,m) with k,l,m in Z and -5≤k,l,m≤5. As such, there are 113=1331 pearls. On the rendering above, the viewer is situated at (3/2,3/2,-3/2) and looks at the pearl which is situated at the origin. The light source is located at (15,15,15).
On the rendering below the viewer is situated at (1/4,1/4,-1/4) and looks at the central pearl with the whole net containing 4913 pearls, instead of 1331. The complexity of the resulting image has increased phenomenally.






Indra's Net is a fractal because it satisfies various conditions of self-similarity. Further, the reflections/refractions on any specific pearl change as the viewing angle changes and as the total number of pearls changes.
An interesting thing with Indra's Net is the question what is it really that gets reflected on those surfaces (or refracted inside the pearls) or that which we see there.
A completely reflective sphere in void space is basically invisible in the absence of any external objects. In other words what the viewer sees on its surface, is only what gets reflected against it. But on every surface are reflected other such spheres, for which the same assumption holds (i.e. they are invisible).
This is true for every reflection on every sphere, ad infinitum, so if one excludes the images of the sphere boundaries which are visible because the rendering program forces some ambient light and some diffusion, it would appear that the image shown on any particular surface is basically a complex light pattern created by the only light source that exists on the scene. In other words, what we see is infinitely many copies of the light source.
Assuming the light source is point-like/dimensionless, if the net extends to infinity, those patterns are fractal Cantor dust for the Pole figure of the diamond lattice (see figure above).
Note that it is fairly easy to see that not every other pearl is reflected directly against a particular pearl in a mirrored net. There are particular sequences of pearls which are not reflected directly on specific pearls.
For this, let us label the pearls as Sr(k,l,m), where r is the radius and (k,l,m), k,l,m in Z, is the pearl's center and let us look at the pearl which is situated at the origin, Sr(0,0,0). Then the following sequences of pearls will NOT be reflected directly on Sr(0,0,0) for example, no matter what the radius r is:
The reason the above sequences of pearls do not get reflected directly on Sr(0,0,0) is fairly obvious: There exists a pearl next to Sr(0,0,0) which because of perspective completely blocks the entire corresponding sequence. There is a total of 26 "blocking" pearls, which are the immediate neighbors of Sr(0,0,0).
The directions of the above sequences of pearls can be seen on the following figure:
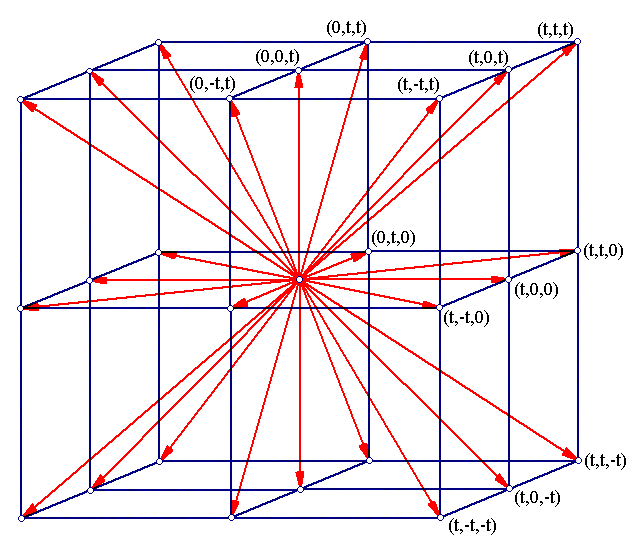
Careful on the qualification "directly". Although for example pearls {Sr(t,0,0): t>1} are not reflected on Sr(0,0,0) directly, they can be reflected directly on Sr(0,0,-1) for example, which in turn is reflected directly on Sr(0,0,0). So "not reflected directly on Sr(0,0,0)" is not the same as "not reflected at all on Sr(0,0,0)".
The exact condition for this "indirect" reflection to occur, is that the blocked sequence pearls {Sr(t,0,0): t>1} are reflected directly on Sr(0,0,-1). For this to occur, if θ is the "viewing angle" of those pearls (as seen from Sr(0,0,-1)), we must have min≤θ≤max, for some values min and max.
Min and max can be calculated using geometry, as functions of the pearl radius r:
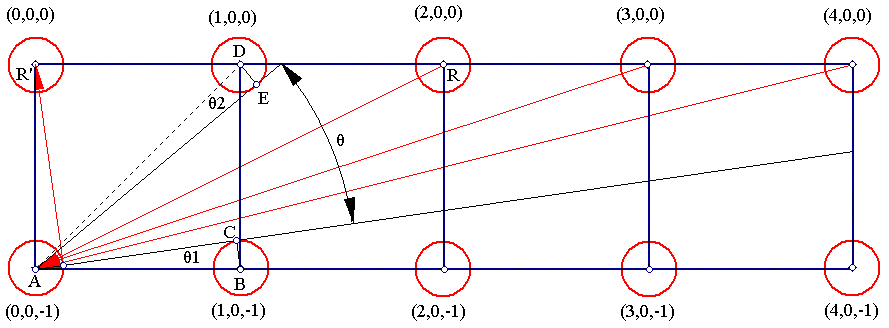
min=θ1, so from the Pythagorean Theorem on triangle ABC: AC2+BC2=AB2 => AC2+r2=1 => AC=sqrt(1-r2) =>θ1=arctan(r/sqrt(1-r2)).
max=π/4-θ2, so similarly from the Pythagorean Theorem on triangle ADE: AD2=AE2+DE2 => 2=AE2+r2 => AE=sqrt(2-r2) => θ2=arctan(r/sqrt(2-r2)) => max=π/4-arctan(r/sqrt(2-r2)).
Consequently, a blocked pearl in the sequence {Sr(t,0,0): t>1} is reflected on Sr(0,0,-1) and finally on Sr(0,0,0) if:
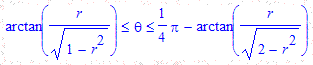
Graphing the two functions min and max, we see the viewing angle θ:
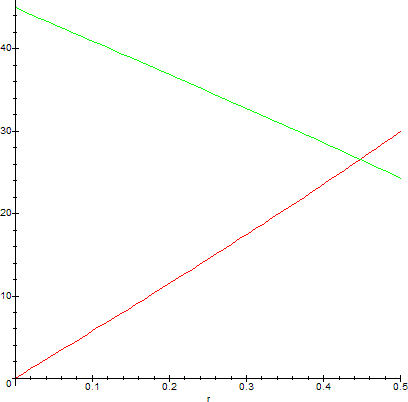
The two graphs intersect at r=0.4472135955. When the pearls have this radius, the central part (on this plane) of Sr(2,0,0) is reflected directly on Sr(0,0,-1), but this reflection does not reach Sr(0,0,0). Other (lower) parts of the pearl Sr(2,0,0) (like R) may, however, be reflected directly on Sr(0,0,-1) and thus eventually may be reflected on Sr(0,0,0) (as R'):
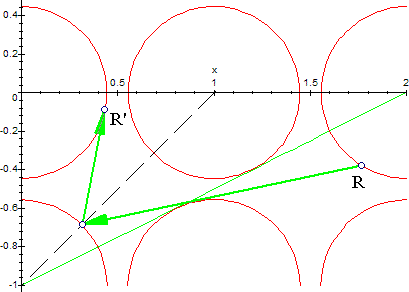
For a given radius r, the furthest pearl from the "blocked" sequence {Sr(t,0,0): t>1} which gets reflected indirectly on Sr(0,0,0) through pearl Sr(0,0,-1), will be such that tan(θ1)=1/t => t=1/tan(θ1) => t=sqrt(1-r2)/r. For r=1/10, for example the previous gives t=9.949874371, so all blocked pearls {Sr(t,0,0): (1<t≤9)} will be reflected (totally or partially) on Sr(0,0,-1) and thus these pearls will eventually be reflected on Sr(0,0,0).
In general and for small values of r, the vast majority of the rest of the pearls do get reflected directly or indirectly on Sr(0,0,0), so the resulting image can be breathtaking.
If one considers Indra's Net to consist of glass pearls instead[2], the situation is very much improved: The blocked sequences of pearls above now become visible through the 26 immediate neighbors via refraction.
The situation can be further improved by allowing for a net which is both reflective and refractive. If you look carefully at the glass pearls in the images above, you will see some very faint reflections as well[3].
Here are four Indra pearls arranged into a tetrahedral cannon-ball pile configuration. The generated fractal is commonly known as Wada's fractal:

Consult the author's YouTube channel for a low quality[4] 3D Flyby in Primordial Chaos with Indra's Net video.