Optical Analysis of an Ornamental Rectangular Prism

Version 1.1 of 4/5/2006-9:50 a.m.

ornamental rectangular pres-papier prism

On Christmas Day one of the visitors brought as a gift to our household a bottle of Johnnie Walker whiskey. The bottle contained a beautiful rectangular prism, presumably to be used as a pres-papier.

The prism consists of high quality crystal/glass and has internally etched the figure of Johnnie Walker. The author was curious as to what it consisted of, so he set forth to measure its index of refraction.

All angles of the prism are 90° (and those which are not are not optical quality) so one has to employ some special tricks. The only things that were actually needed for the measurement were a laser pointer, a ruler and a piece of paper. The analysis can be summarized in the following diagram:

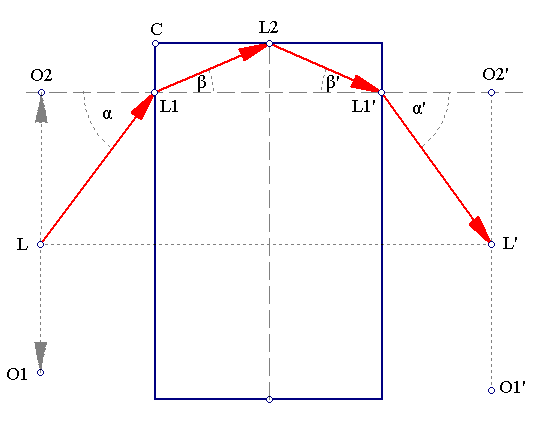
prism tracing diagram

Let us follow the actual analysis:

  1. Let the prism rest on its long side atop some A4 paper, with one paper fold running parallel to the long edge. This is axis O1'O2'.
  2. Move the Laser pointer along axis O1O2, keeping its angle to the normal L1O2 always constant, until the Laser image L' emerges on paper O1'O2', and until O2'L'=O2L.
  3. At this point, α=α', β=β' and the perpendicular at L2 bisects the reflection angle of the Laser path.
  4. We have: tan(α)=LO2/O2L1=5.5 cm/7 cm, hence α=0.66596 rad.
  5. We also have: tan(β)=CL1/CL2=1/4.9/2 cm, hence β=0.38752 rad.
  6. The Laser diode emits at 660 nm (see spectrum [1.7.2]), hence n660=sin(0.66596)/sin(0.38752)=1.63489.
  7. We check the list of refractive indexes on Wikipedia (figure), and see that for λ=660 nm this is very close to flint glass.

A very interesting and beautiful little ornament. Measuring also the dimensions of the prism, we get H~8 cm, W~4.9 cm and L~4.9 cm, hence its volume is V~192 cm3. Dividing its weight, 480 gr, by the volume, we get the crystal's density, D~ 2.5 gr/cm3. Regular glass has a density of ~2.2 gr/cm3, so the ornament is indeed close to crown or flint glass.

The process used to manufacture this ornament is a scientific feat by itself:

  1. First the glass is melt and a glass block is roughly shaped at or around some ideal working temperature (usually 800-900° for quartz).
  2. The block is then shaped into a prism by careful polishing of its major edges, to some acceptable optical quality.
  3. The optical quality has to be sufficient for Sub Surface Laser Engraving to take place (section SSLE), which is how the Johnnie Walker figure is engraved into the crystal's internals.

As the author understands it, this particular type of internal engraving, uses multiple lasers which individually have power loads less than the damage threshold of the crystal (hence individually they cannot damage it). When used combined and focused on a specific point, the total power load exceeds the crystal's damage threshold, hence with very careful and accurate focusing a small three-dimensional matrix can be etched in the crystal's insides.