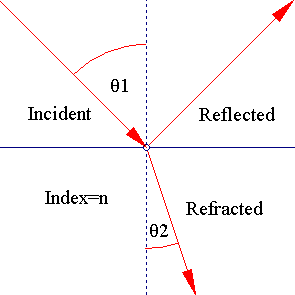
When eyeglass-wearer astronomy amateurs observe through their scopes they usually take their glasses off. However for some of us with astigmatism this is not possible since no scope offers astigmatism correction. Since every optical surface introduces some reflection, it is wise to choose one's spectacle substrate carefully when one is an amateur astronomer. Let us then follow some simple observations on what spectacle substrates are best suited for amateur astronomers with corrective eyeglasses.
Our objective is to investigate what the best choice of substrates for our eyeglasses is.
The investigation starts with the fresnel equations as they are derived from solutions to Maxwell's equations for his electromagnetic theory of light:
Rp = tan2(θ1-θ2)/tan2(θ1+θ2)
(1) and
(1) and (2) give the reflection coefficients Rp and Rn for the p-vibrations and the n-vibrations respectively in the following situation:

Using:
θ2=arcsin(sin(θ1)/n) (3),
The reflection coefficient of natural light will then be:
Rnat = [Rp+Rn]/2 (4)
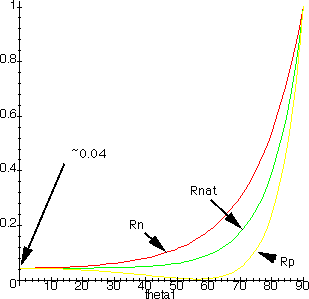
The reflection coefficients are functions of not only θ1 but of the index of refraction, n. So we can see how all three components behave as functions of both θ1 and n.
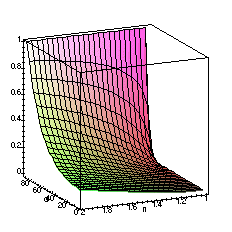
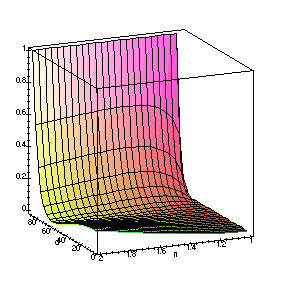
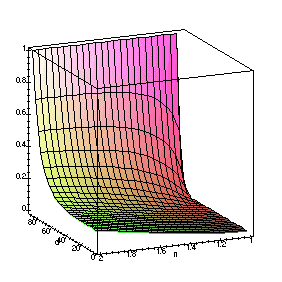
The above graphs show clearly the behavior of all three components. It is clear that reflection increases as n goes up, except when θ1 is close to the brewster's angle for the substrate.
Since we will be looking through a scope, we are essentially interested in restricting the above investigations to θ1 = 0°. However, θ1 = 0 gives an indeterminate form of 0/0 in (1), so we need to examine (1) a bit better.
We attack (1) through L'hospital and indeed a nice result comes out:
Differentiating tan(θ1-θ2) and tan(θ1+θ2) and plugging in θ1 = 0, yields:
d[tan(θ1-θ2)]/dθ1|0 = 1-1/n (5)
similarly:
d[tan(θ1+θ2)]/dθ1|0 = 1+1/n (6)
Accordingly then:
Rp = [(n-1)/(n+1)]2 (7)
Doing the same to Rn we get similarly:
Rnat = [(n-1)/(n+1)]2 (9)
So we only need investigate (9).
Here then is the graph of Rnat as a function of n when the incidence angle is 0:
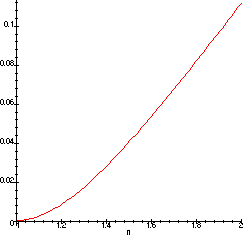
And the above is the information we need. It is immediately obvious that as the refraction index increases, so does the reflection coefficient Rnat.
A quick check with the local optician, reveals some of the available glass substrates, with indexes, n=1.807, n=1.706, n=1.6, n=1.5 and some of the available plastic substrates with indexes, n=1.56 and n=1.65. Plugging in for Rnat in (9) we get:
| n | Rnat |
| 1.807 | 8.2% |
| 1.706 | 6.8% |
| 1.6 | 5.3% |
| 1.5 | 4% |
| 1.56 | 4.7% |
| 1.65 | 6% |
It becomes apparent thus, that the least reflection takes place when
the index of refraction is lowest. However, this is not really news.
Can
we improve the situation by applying various coatings on the lenses?
Yes
we can. We consider the three broadband anti-reflective coatings: ARB1,
ARB2 and ARB3 which have a residual reflectance of 1.3%, 0.3% and 1%.
Then
the reflection coefficients will give:
| n | Rnat | RnatARB1 | RnatARB2 | RnatARB3 |
| 1.807 | 8.2% | 2.9% | 0.059% | 0.19% |
| 1.706 | 6.8% | 2.4% | 0.048% | 0.16% |
| 1.6 | 5.3% | 1.9% | 0.038% | 0.12% |
| 1.5 | 4% | 1.4% | 0.028% | 0.09% |
| 1.56 | 4.7% | 1.7% | 0.034% | 0.1% |
| 1.65 | 6% | 2.1% | 0.042% | 0.1% |
It is now obvious that the situation is improved dramatically. Dense flint spectacles with ARB1 anti-reflective coating perform better than all plain substrates. So here a personal choice needs to be made that offers some sort of compromise between lens value (as n goes up the glasses are more expensive) and performance.
Here's then a comparative graph of all 4 substrates, plain glass, coated with ARB1, ARB2 and ARB3 coatings as a function of the refraction index:
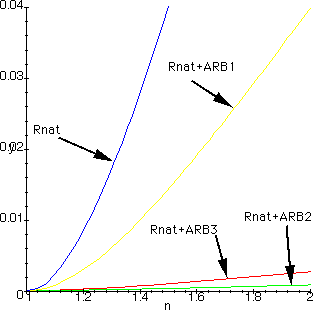
Some obvious comparisons are easy: A substrate of index n=2 coated with ARB1, performs as good as an un-coated substrate of index n=1.5 for example and a substrate of index n=2 coated with ARB2 performs as good as an un-coated substrate of index n=1.057 !!
The ideal choice, then, would be of course the n=1.5 substrate with the ARB2 anti-reflective coating. The coatings above are picked from reference [3], as such they may not be available at your optician. However, most optical stores do offer at least one kind of anti-reflective coating and usually publish the reflection curves, so if you are an eyeglass wearer and amateur astronomer you should always get coated lenses of the least refractive index coated with a broadband anti-reflective coating with the lowest residual reflectance.
Some opticians offer anti-reflective coatings even on plastic lenses, so a wise choice would be plastic or crown glass coated substrates if your myopia or hypermetropia is not too high (up to 5.0-6.0) or denser coated glasses if your myopia or hypermetropia is relatively high.