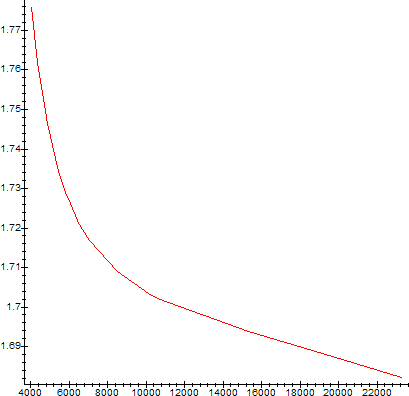
Graph of Sellmeier's Equation for the SF10 Crystal
| λ (A) | Element | nλ |
| 23254 | Hg arc | 1.68218 |
| 19701 | Hg arc | 1.68750 |
| 15296 | - | 1.69378 |
| 10600 | Nd laser | 1.70227 |
| 10140 | Hg arc | 1.70345 |
| 8521.1 | Cs arc | 1.70889 |
| 7067.217 | Ar arc | 1.71682 |
| 6562.8 | H arc | 1.72085 |
| 6438.4696 | Cd arc | 1.72200 |
| 6328 | HeNe laser | 1.72309 |
| 5892.938 | Na arc | 1.72803 |
| 5875.618 | He arc | 1.72825 |
| 5460.74 | Hg arc | 1.73430 |
| 4861.327 | H arc | 1.74648 |
| 4799.9107 | Cd arc | 1.74805 |
| 4358.35 | Hg arc | 1.76197 |
| 4046.561 | Hg arc | 1.77578 |
All the calculations below are valid only for the area of the sodium D lines.
PHASMATRON dn/dλ:
First from the table of the SF10 prism we get:
dn/dλ~Δn/Δλ=(1.72825-1.72803)/ |5875.618-5892.938|A=1.2702*10-5/A.
dn/dλ~1.2702*10-5/A. (In the area of the sodium D lines)
Then, the resolving power (or separation limit) Δλ is defined by the Lord Rayleigh"s formula as Δλ=λ/{B(dn/dλ)} where B is the length of the prism Base (in Angstroms).
PHASMATRON Resolving power: Δλ=λ/{B(dn/dλ)}
For the sodium D area we get:
λ=5892.938A,
B=2*6*108A, (1cm=108A, 2 prisms x 6cm Base each),
dn/dλ =1.2702*10-5/A, =>
Δλ=0.3866148Angstroms. (In the area of the sodium lines)
If you work in the sodium D area observe that the sodium D line is actually two lines with wavelengths D1=5895.923A, D2=5889.953A. The phasmatron spectroscope will easily resolve them, since their corresponding difference of 5.97A is greater than Δλ=0.3866148A.
The resolution is then defined to be R=λ/Δλ, so
PHASMATRON Resolution: R=λ/Δλ
For λ=5892.938A, and
Δλ=0.3866148A,
R=15242.4. (In the area of the sodium lines)
Then consider the formula of minimum deviation angle for one prism:
sin{(D+A)/2}/sin{A/2}=nλ. (1)
(where D is the minimum deviation angle, and A is the apical prism angle). The
phasmatron has 60 degree prisms so A=60°. But we cannot apply the formula above
directly, because the two prism geometry is different from the one prism case. What we
CAN do however, is calculate the dispersion of the system, which is defined as
dE/dλ. For the one prism case it is easy to see that in the position of minimum
deviation, we can differentiate (1) to get:
cos{(D+A)/2}(dD/dn)(1/2)=sin{A/2} =>
dD/dn=2sin{A/2}/cos{(D+A)/2} (2)
Given that (1) => (D+A)/2=sin-1{nλ*sin{A/2}}
(2) => dD/dn=2sin{A/2}/cos{sin-1{nλ*sin{A/2}}} (3)
since here A=60°, (3) =>
dD/dn=1/cos{sin-1{nλ/2}}
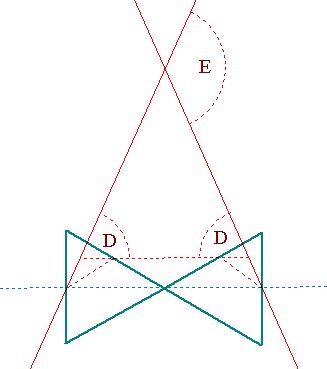
However note that E=2D so dE/dn=2*dD/dn
Using (3) we get for nD=1.72803, dD/dn=1.9869763 rad.
For the PHASMATRON which has two prisms, we thus get:
PHASMATRON dE/dn=2dD/dn=2/cos{sin-1{nλ/2}}:
for nλ=1.72803, =>
dE/dn=3.9724624 rad.
Accordingly we now define dispersion:
PHASMATRON dispersion: dE/dλ=(dE/dn)(dn/dλ):
for dn/dλ=1.2702*10-5/A
for dE/dn=3.9724624 rad, =>
dE/dλ=5.04582*10-5 rad/A.
On the photographic plate we also define the dispersive power usuful in
creating scales. We need to know how many mm"s of film fit in an Angstrom under the
current circumstances. This is expressed as:
PHASMATRON dispersive power: ds/dλ=f*(dE/dλ).
where f is the camera"s lens focal length, using camera lens in front of prism.
For example:
| f: | ds/dλ: | dλ/ds: |
| 50mm | 2.52291*10-3mm/A | 396.36A/mm |
| 135mm | 6.81185*10-3mm/A | 146.80A/mm |
| 300mm | 0.0151374mm/A | 66.06A/mm |
| 700mm | 0.0353207mm/A | 28.31A/mm |
Next we calculate the angle of the spectrum:
PHASMATRON spectrum angular width: ΔE=(dE/dn)Δn.
We take Δn=1.77578-1.71682, the limits of the visible spectrum.
dE/dn=3.9724624 rad, =>
ΔE=13.42°. (As we shall see this is not entirely accurate, since dE/dn is
valid only in the area of the sodium D lines, and not on the entire spectrum. In fact,
the true width will be around 16.84° owing to correct measuring of the internal
angles. See section on Spectrum
Angular Width).
Next, the width of the entire spectrum on the film can be calculated.
PHASMATRON width of spectrum on film: Δs=f*ΔE
where f is the focal length of the lens used on the camera.
take f=50mm,
ΔE=16.84°=0.2939134 rad, =>
Δs=14.69567mm on film.
If we took instead f=700mm then
Δs=205.73938mm on film. (See also section on Phasmatron Photography).
Next we indicate some common constants of the SF10 crystal:
nF, nC, nD, are the refraction indexes for the
Hydrogen F, C lines and the sodium D line. (4861.327A=F, 6562.8A=C, 5892.938=D)
(nF- nC) is called the mean dispersivity
for nF=1.74648, nC=1.72085 and nD=1.72803
we get:
SF10 mean dispersivity: (nF- nC)=0.02563
Let ω=(nF- nC)/(nD- 1)=0.0352045. ω is the
inverse of the Abbe number.So:
SF10 Abbe # =1/ω=28.405384.
The Brewster angle is the angle for which the reflected beam is totally
linearly polarized.
SF10 Brewster angle: θ=tan-1(nλ).
for nλ=1.72803, =>
θ=59.945468° (for sodium light)
Next, the internal transmittance table for the SF10 crystal follows:
|
λ (nm)
|
Ti (5mm)
|
|
2325.4
|
0.959
|
|
1970.1
|
0.990
|
|
1529.6
|
0.999
|
|
1060.0
|
0.999
|
|
700
|
0.999
|
|
660
|
0.999
|
|
620
|
0.999
|
|
580
|
0.999
|
|
546.1
|
0.999
|
|
500
|
0.998
|
|
460
|
0.995
|
|
435.8
|
0.990
|
|
420
|
0.981
|
|
404.7
|
0.952
|
|
400
|
0.93
|
|
390
|
0.83
|
|
380
|
0.59
|
|
370
|
0.21
|
|
365.0
|
0.06
|
To find the internal transmittance for a block of thickness K other than 5mm use the
following formula[2]:
SF10 internal transmittance :
Ti(Kmm)=Ti(5mm){K/5}
For example the internal transmittance for 25mm for the 420nm line will be[3]:
T420(25mm)=0.981{25/5}=0.9815=0.908542.