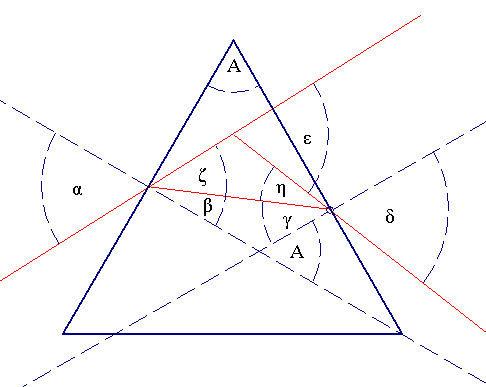
Deviation Diagram for a Prism
The total deviation ε of a light ray refracted through a prism can be calculated, given the incidence angle α. The same calculation allows for determination of the emergence angle δ.

We have:
ε=ζ+η
A=β+γ
=>A+ε=(ζ+β)+(γ+η)
=>A+ε=α+δ
=>ε=α+δ-A (1)
sin(δ)/sin(β)=n=>δ=arcsin{n*sin(β)}
β=A-γ
=>δ=arcsin{n*sin(A-γ)} (2)
β=arcsin{sin(α)/n}, because sin(α)/sin(β)=n again,
so (2)=>δ=arcsin{n*sin[A-arcsin(sin(α)/n)]} (3)
Now
sin[A-arcsin(sin(α)/n)]=sin(A)*cos(arcsin(sin(α)/n))-cos(A)*sin(α)/n
So δ=arcsin{n*sin(A)*cos(arcsin(sin(α)/n))-cos(A)*sin(α)}
=arcsin{n*sin(A)*Ö[1-(sin(α)/n)2]-cos(A)*sin(α)}
=>δ=arcsin{sin(A)*Ö[n2-sin2(α)]-cos(A)*sin(α)} (4)
And finally:
(1)(4)=>
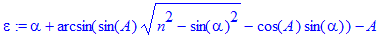 (5)
(5)
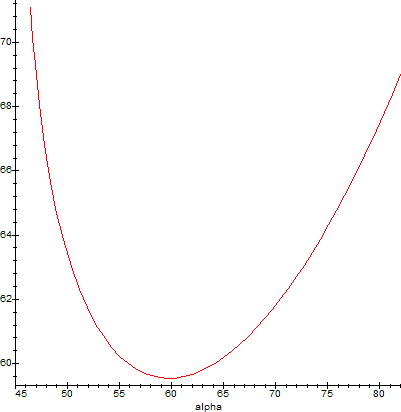
Here's a graph of the above equation, with A=60°, nD=1.72803 (SF10 Crystal) and α ranging from 45° to 80°. Angles are measured in degrees on the graph. Note that the deviation has a minimum, close to 60°. This fact can also be experimentally demonstrated using the angle readers of a spectroscope or numerically simulated (as in reference [2]).
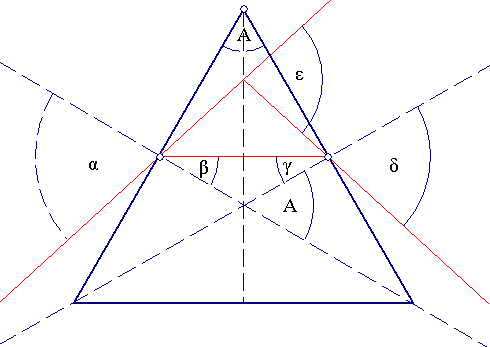
For the position of minimum deviation, the ray travels perpendicular to the bisect
of angle A, and incidence and emergence angles are equal. Then:
α=δ and β=γ (6)
Also: A=β+γ, εmin=(α-β)+(δ-γ)
(7)
(7)(6)=>A=2*β, εmin=2*α-2*β or
β=A/2 and εmin/2=α-A/2 =>
α=εmin/2+A/2 (8)
Now we know that n=sin(α)/sin(β) so from the last equation and (8) we
get:
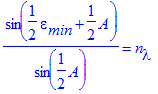 (9)
(9)
For nD=1.72803 and A=60°, expression (9) gives εmin=59.54084145°, which is exactly the minimum displayed on the graph above.
The actual proof that the angle εmin given by (9) is in fact the minimum of (5) is very complicated (it can be found in [3], page 81). It can be proved using calculus, that if α is a root of the equation: dε/dα=0, with ε given by (5), then ε(A,n,α)=2*arcin(n*sin(A/2))-A=εmin. A proof using Maple 9 commands, is provided courtesy of Robert Israel. After you execute the commands, try to understand why this is a perfectly valid proof.
> epsilon:=(A,n,alpha)->alpha+arcsin(sin(A)*sqrt(n^2-sin(alpha)^2)-cos(A)*
sin(alpha))-A;
> S:= solve(diff(epsilon(A,n,alpha),alpha),alpha);
> S5:= simplify(S[5]) assuming n > 1, A > 0, A < Pi/2;
> Q:=sqrt((1-cos(epsilon(A,n,S5)+A))/2) - n*sqrt((1-cos(A))/2);
> Q:= simplify(expand(Q)) assuming n>1,A > 0,A < Pi/2;
> simplify(combine(Q)) assuming A > 0,A < Pi/2,n > 1;
Because the light dispersion angle is very small, (on the order of 7°) practically all the rays suffer minimum deviation. When a prism spectroscope is designed, its prism is placed in that position for usually the yellow part of the spectrum. (Sodium D lines). The PHASMATRON's prisms are placed in minimum deviation position for the green line of λ=5615.97363281Angstroms, its resonating wavelength.
References: