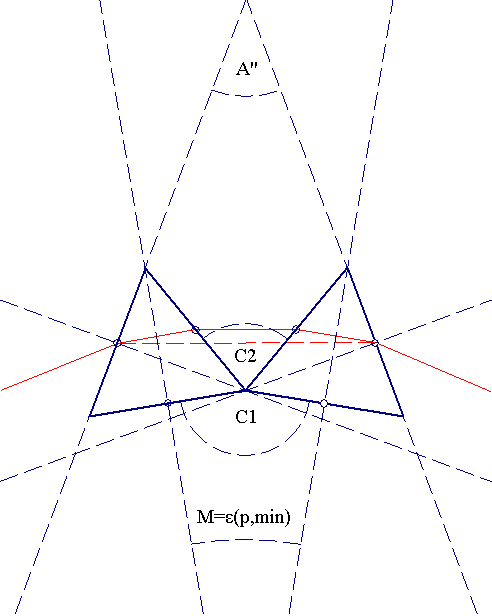
Let us consider a system of two identical prisms, of apical angles A, and of refractive index n_p, placed in a position where they both disperse a ray of light passing through them, as in the above figure. Let the angle between them be M. The system of two prisms, amounts to an imaginary prism A''BB' with apical angle A'', and refractive index n_2p. We have for the minimum deviation angle for one prism:

ε_p,min=2*arcsin{n_p/2}-60° (1)

This comes from the minimum deviation formula for one prism:

n_p=sin{(ε_p,min+A)/2}/sin(A/2) (A=60°) (2)

For an equivalent imaginary prism, the same formula applies, but with changed ε and A. In that case:

n_2p=sin{(ε_2p,min+A'')/2}/sin(A''/2) (3)

Now in order to calculate with (3) we need ε_2p,min and A''. It can be shown using geometry that M=ε_p,min (4)

Now, A''+240°+C2=360° =>A''=120°-C2, C2+C1+120°=360° =>C2=240°-C1 =>A''=C1-120° (5)

Next, C1+180°+ε_p,min=360°=>C1+180°+ε_p,min=360°=>C1=180°-ε_p,min (6)

(5)(6)=>A''=180°-ε_p,min-120°=>A''=60°-ε_p,min (7)

We also have: ε_2p,min=2*ε_p,min (8)

(3)(7)(8)=>n_2p=sin{(2ε_p,min+60°-ε _p,min)/2}/sin{(60°-ε_p,min)/2}=> n_2p=sin{(ε_p,min+60°)/2}/sin{(60°-ε_p,min)/2} and using equation (2) => n_2p=(n_p/2)/sin{(60°-ε_p,min)/2} => n_2p=(n_p/2)/sin{30°-ε_p,min/2} (9)

Using (1) we get:

(9)(1) =>n_2p=(n_p/2)/sin{30°-arcsin(n_p/2)+30°}=> n_2p=(n_p/2)/{sin60°cos[arcsin(n_p/2)]-cos(60°)*(n_p/2)}, which becomes n_2p=(n_p/2)/{sqrt(3/2)*sqrt(1-(n_p/2)²)-n_p/4}, which after simplifications becomes:

n_2p={sqrt(3/2)*sqrt((2/n_p)²-1)-1/2}^-1 (10)

The function's graph is shown on the following figure:

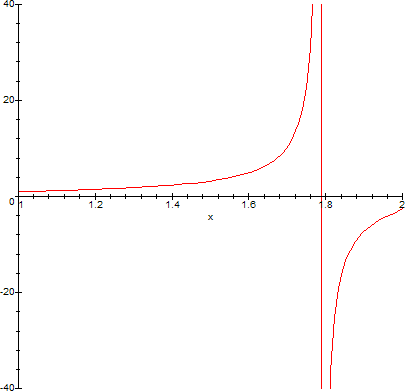
It has a singularity exactly at n_p=sqrt(3), since then, n_2p->∞. Note that the system doesn't make sense for n_p>2 so the domain of the function is precisely the set {1<n_p<sqrt(3)} U {sqrt(3)<n_p<2}.

Since at n_p=sqrt(3) the prisms are in such positions of minimum deviation that M=60°, the system resonates at that point. Below sqrt(3) the quantity n_2p is positive, above, negative, to reflect the fact that there is no equivalent prism, since the apical angle is essentially negative. The frequency of resonance can be found using interpolation, or the program on Measuring Wavelengths section. It is N=60°, M=60°, λ=5615.97363281 Angstroms.

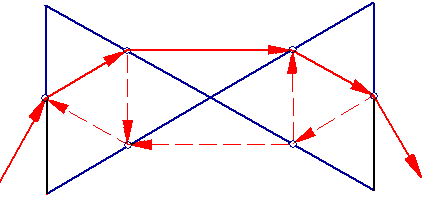
System resonance is shown on the figure, above. When it happens, the ghost image for λ=5614.97363281 Angstroms coincides with the real image for the same wavelength.