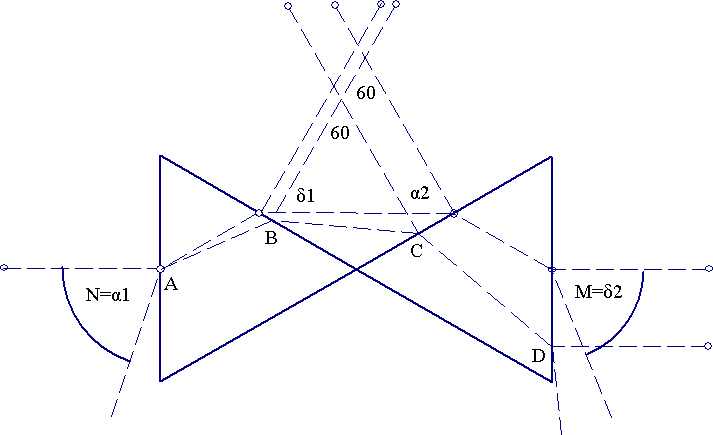
The following calculations assume you have read the analysis on Calculating the Deviation Angle For a Prism.

Suppose we can measure a₁=N, and δ₂=M. Then if the incidence angle at A is a₁ then the emergence angle at B will be such that:

δ₁=arcsin{sin(A)*sqrt(n_λ²-sin²(a₁))-cos(A)*sin(a₁)} (1)

Similarly, tracing the ray backwards, if the incidence angle at D is δ₂ then we have an emergence angle α₂ at C, for which:

α₂=arcsin{sin(A)*sqrt(n_λ²-sin²(δ₂))-cos(A)sin(δ₂)} (2)

We also have: δ₁+α₂=120° (3)

=>sin(δ₁)=sin(120°-α₂)

=>sin(δ₁)=sin(120°)*cos(α₂)-cos(120°)*sin(α₂), and upon evaluating,

=>sin(δ₁)=sqrt(3/2)*sqrt(1-sin²(α₂))+1/2*sin(α₂), and upon substitution of (1) and (2) =>

sqrt(3/2)*sqrt(n_λ²-sin²(δ₂))-sin(δ₂)/2=sqrt(3/2)*sqrt{1-(sqrt(3/2)*sqrt(n_λ²-sin²(δ₂))-sin(δ₂)/2)²}+1/2{sqrt(3/2)*sqrt(n_λ²-sin²(δ₂))-sin(δ₂)/2}.

Now consider f(n,N,M) defined as above. Namely: f(n,N,M) = sqrt(3/2)*sqrt(n-sin²(N))-sin(N)/2-sqrt(3/2)*sqrt{1-(sqrt(3/2)*sqrt(n-sin²(M))-sin(M)/2)²}-1/2{sqrt(3/2)*sqrt(n-sin²(M))-sin(M)/2}

This can be solved for n given the angles N, and M, using Newton's iteration as n_(k+1)=n_k-f(n_k,N,M)/f'(n_k,N,M), where f' is the function's derivative at n_k.

Then having a convergence value n, we can interpolate as follows:

y=(n-n_λ1){(λ1-λ2)/(n_λ1-n_λ2)}+δ₁, where n_λ1<n<n_λ2 are the nearest refraction index bounds from the table for the SF10 crystal.

A Pascal program which calculates the wavelength given N and M follows:

 program SolveEqu;
 const
  epsilon = 1e-5;
  firstguess = 1.8;
 var
  i: integer;
  xn, N, M, ac, x, x1, x2, y1, y2: real;
 function f (x: real): real;
  var
   a, b, c: real;
 begin
  a := ac * Sqrt(Sqr(x) - Sqr(Sin(M))) - Sin(M) /2;
  b := ac * Sqrt(1 - Sqr(ac * Sqrt(Sqr(x) - Sqr(Sin(N))) - sin(N) /2));
  c := 0.5 * (ac * Sqrt(Sqr(x) - Sqr(Sin(N))) - sin(N) /2);
  f := a - b - c;
 end;
 function df (x: real;
   epsilon: real): real; {the function's derivative}
 begin
  df := (f(x + epsilon) - f(x)) /epsilon;
 end;
 begin
 write('Enter entrance Angle:');
 readln(N);
 write('Enter exit Angle:');
 readln(M);
 xn := firstguess;
 ac := Sqrt(3) /2;
 N := pi * N /180;
 M := pi * M /180;
 for i := 1 to 5 do   {Newton iteration}
  xn := xn - f(xn) /df(xn, epsilon);
 write('After ', i - 1 : 1, ' iterations, the equation converges to:');
 writeln(xn : 3 : 8);
 if (1.70889 < xn) and (xn <= 1.71682) then
  begin
   x1 := 7067.217;
   y1 := 1.71682;
   x2 := 8521.1;
   y2 := 1.70889;
  end
 else if (1.71682 < xn) and (xn <= 1.72085) then
  begin
   x1 := 6562.8;
   y1 := 1.72085;
   x2 := 7067.217;
   y2 := 1.71682;
  end
 else if (1.72085 < xn) and (xn <= 1.72200) then
  begin
   x1 := 6438.4696;
   y1 := 1.72200;
   x2 := 6562.8;
   y2 := 1.72085;
  end
 else if (1.72200 < xn) and (xn <= 1.72309) then
  begin
   x1 := 6328;
   y1 := 1.72309;
   x2 := 6438.4696;
   y2 := 1.72200;
  end
 else if (1.72309 < xn) and (xn <= 1.72803) then
  begin
   x1 := 5892.938;
   y1 := 1.72803;
   x2 := 6328;
   y2 := 1.72309;
  end
 else if (1.72803 < xn) and (xn <= 1.72825) then
  begin
   x1 := 5875.618;
   y1 := 1.72825;
   x2 := 5892.938;
   y2 := 1.72803;
  end
 else if (1.72825 < xn) and (xn <= 1.73430) then
  begin
   x1 := 5460.74;
   y1 := 1.73430;
   x2 := 5875.618;
   y2 := 1.72825;
  end
 else if (1.73430 < xn) and (xn <= 1.74648) then
  begin
   x1 := 4861.327;
   y1 := 1.74648;
   x2 := 5460.74;
   y2 := 1.73430;
  end
 else if (1.74648 < xn) and (xn <= 1.74805) then
  begin
   x1 := 4799.9107;
   y1 := 1.74805;
   x2 := 4861.327;
   y2 := 1.74648;
  end
 else if (1.74805 < xn) and (xn <= 1.76197) then
  begin
   x1 := 4358.35;
   y1 := 1.76197;
   x2 := 4799.9107;
   y2 := 1.74805;
  end
 else if (1.76197 < xn) and (xn <= 1.77578) then
  begin
   x1 := 4046.561;
   y1 := 1.77578;
   x2 := 4358.35;
   y2 := 1.76197;
  end
 else
  writeln('refraction index out of bounds.');
 if (1.70889 <= xn) and (xn <= 1.77578) then
  begin
   x := (xn - y1) * (x1 - x2) /(y1 - y2) + x1;
   writeln('Estimated wavelength:', x : 3 : 8);
  end;
 end.

Using the Phasmatron spectroscope,

1. Rotate the viewing telescope until the line desired is centered in your field of view.
2. Read the angle readers.
3. Run the program on a PC, and input the two angles, N of the collimator, M of the viewing telescope. The desired wavelength will be output after the program is run.

We can also use the above program to improve accuracy on itself. However this will require that we know how to program a computer to change slightly the structure of the program above. Note that the table of refractive indexes is quantized. That is, only specific wavelengths have their refractive index noted. We can augment the table above, and insert new points, by measuring the index of some otherwise known wavelength. For example: If we know that Cadmium emits a line also at 4511.34A, we can use a Cadmium discharge lamp, and center the line on the Phasmatron spectroscope's field of view. Then we run the program on the PC to measure the index of refraction for this line. The index we get along with the exact wavelength of 4511.34A, constitutes a new point on the SF10 refractive index table, so we can add it there. We don't use the estimated wavelength from the program's run; we use only the index of refraction. Then we can change the program to interpolate not between 1.76197 and 1.74805, but between 1.76197 and the new refraction index value, and between the new value and 1.74805 (since 4511.34 falls between 4358.35 and 4799.9107A).