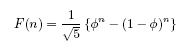
The Golden Ratio and Other Metal Ratios

The Golden Ratio, φ=(1+sqrt(5))/2 arises in connection with the Fibonacci Sequence.

The Fibonacci sequence is defined as: F(n+2) = F(n+1) + F(n), with F(0) = 0 and F(1) = 1. To solve the recurrence explicitly, one observes that a solution which satisfies the recurrence has to satisfy the characteristic equation xn+2 = xn+1 + xn, or the equation: x2 = x + 1, from which we get: x1,2 = φ, 1-φ.

The general solution to the recurrence, then, will be F(n) = a*φn + b*(1-φ)n, where a and b are constants. a and b have to satisfy the initial terms as F(0) = 0 and F(1) = 1, from which we get the Binet expression, which solves the Fibonacci recurrence explicitly:

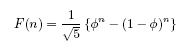
Binet expression for Fibonacci
Interesting variations come about when we consider the recurrence F(n+2) = p*F(n+1) + q*F(n), with F(0) = 0 and F(1) = 1 and p,q in {1,2,3,4,...}. Following exactly similar tactics, this recurrence can be solved explicitly as:
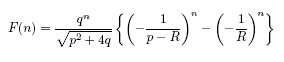
General Binet expression
where now R is a particular "metal ratio". For p=q=1, we get R=φ, the Golden Ratio. For p=3 and q=1, we get the Bronze Ratio, R = 3.302775638. Let's see some of these metal ratios with Maple and the corresponding sequences which are generated by the modified recurrence F(n+2) = p*F(n+1) + q*F(n), with F(0) = 0 and F(1) = 1:

> Rm:=(p,q)->(p+sqrt(p^2+4*q))/2;

> for p from 1 to 3 do
> for q from 1 to 3 do
> print(p,q,evalf(Rm(p,q)));
> od;
> od;

p q R Sloane Sequence Continued Fraction
1 1 φ=1.618033988 (Golden)[1] A000045 [1,1,1,1,1,1]
1 2 2 A001045 [2]
1 3 2.302775638 A006130 [2,3,3,3,3,3]
2 1 1+sqrt(2)=2.414213562 (Silver)[1] A000129 [2,2,2,2,2,2]
2 2 2.732050808 A002605 [2,1,2,1,2,1]
2 3 3 A015518 [3]
3 1 (3+sqrt(13))/2=3.302775638 (Bronze)[1] A006190 [3,3,3,3,3,3]
3 2 3.561552813 A007482 [3,1,1,3,1,1]
3 3 3.791287848 A030195 [3,1,3,1,3,1]

Construction

Metal Ratios can be constructed geometrically: The solutions to the quadratic x2-p*x-q=0, are the points where the circle whose diameter is determined by the points A = (0,1) and B = (-p,q), intersect the x-axis. Indeed, for the Bronze Ratio, we get the following figure using EucliDraw:

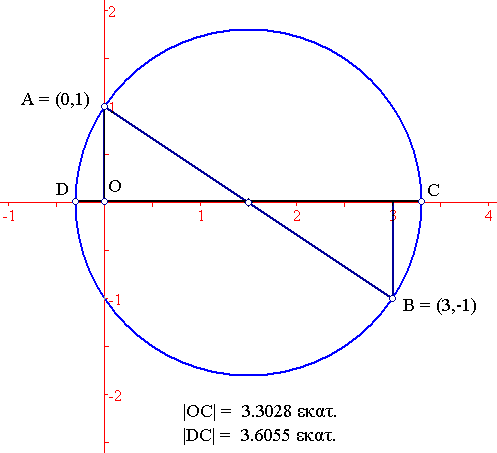
Bronze Ratio construction
Construction of Bronze Ratio

EucliDraw reports: OC ~ 3.3028, while DC ~ 3.6055, hence OD ~ 0.3027. And indeed, the Bronze Ratio is equal to (3 + sqrt(13))/2 ~ 3.302775638, and hence OC and DO are the two roots of the quadratic x2-3*x-1=0.

Notes

  1. To see the spectra of these ratios, consult Google Scholar and the Spectra of the Scientists.