A very elegant construction in Mathematics is the standard Von Neumann construction in set theory which defines the natural numbers in terms of sets. One starts with the empty set 0:
Then one defines the natural number n to be (the cardinality of) the set Sn(0), where S(a) is the successor function defined by S(a)=a U {a} for every set a and the superscript denotes repeated composition. Explicitly:
The above construction is elegant and powerful:
Consider the set of all letter words W of finite length. If i,j in N, w,wi in W, and w[i] denotes letter i of word w, we define the maps C:W->W (the concatenation operator), SS:W x N2 -> W (the substring operator), and L:W->N (the word length operator) in the obvious way:
The map VN(n)=Sn(0) of the Von Neumann construction now induces a natural map VS:N->W, from the natural numbers to the set of words W of finite length, defined by:
VS(n) is essentially the string representation of the Von Neumann set VN(n) minus the commas.
We now define a letter replacement transformation R:W->W as follows:
R basically takes the word w and replaces all occurances of '0', '{' and '}', with '0','1' and '2' respectively.
We next define the map V:W->N as follows:
V basically gives the base 10 value of the number represented by the word w. Finally we look at the sequence defined by:
Here are the terms a(0) to a(7):
a(n) is an interesting sequence. For all n, 2|a(n) and 3|a(n), => 6|a(n). Call D(n) the number of digits of the number n. If n>0, then a(n) always contains D(a(n))/3 0's, 1's and 2's. The word representation of a(n) never contains the patterns {"00","11","12","20"}. It always contains the pattern "2...2" (n 2's) once and always ends with that pattern. a(n)/2 contains only the digits {0,1,5}. a(n)/3 contains only the digits {0,3,4,6,7}. a(n)/6 contains only the digits {0,1,3,5,6,7,8}.
Let's investigate it a little. It is easy to see that D(a(n)) is given (why?) by the recursion:
Solving the recurrence with Maple (or by hand if you are savvy), we get:
> rsolve({K(n)=2*K(n-1),K(1)=3},K(n));
K(n)=3/2*2n, =>
D(a(n))=3/2*2n.
On the other hand, for any natural number n we have: D(n)=[log10(n)]+1,
where [x]=floor(x), =>
[log10(a(n))]+1=3/2*2n, =>
log10(a(n))+1~3/2*2n, =>
log10(a(n))~3/2*2n-1, =>
a(n)~103/2*2n-1.
That's a fast growing sequence! Can we find a nice recursion for a(n)? Look carefully at the function VS, above, and try to convince yourself that the following works:
Because there are always just 3 letters in the final word w ("0", "1", and "2"), one is tempted to define the last function V, alternatively as:
which gives the base 3 value of the number represented by the word w, and then look at b(n) defined similarly:
Here are the terms b(0) to b(7):
It's more or less obvious that b(n) grows slower than a(n). How MUCH slower?
If we call Db(n) the number of digits of the number n in base b, then
D3(n)=[log3(n)]+1. Note however that
D3(b(n))=3/2*2n. (why?). Therefore:
[log3(b(n))]+1=3/2*2n, =>
[log3(b(n))]=3/2*2n-1, =>
log3(b(n))~3/2*2n-1, =>
b(n)~33/2*2n-1.
Therefore b(n) grows much slower than a(n).
a(n) and b(n) made it into Neil Sloane's Encyclopedia of Integer Sequences, as sequences A129751 and A129754.
The natural thing to ask now, is whether 0.a(n) and 0.a(n)3 converge. Let's define those sequences formally. Let D(n) be as above. Then
Here are the first terms of c(n):
and of d(n):
Can we say anything about c(n) and d(n)? Yes!
c(n) converges! For all n we have c(n+1)<c(n) (can you see why?). Furthermore, for all n>0, c(n) is bounded: 0<c(n)<0.102 (why?), hence converges to some number 0<A<0.102 (why?). What about d(n)? It obviously converges to A in base 3 (why?) Can anything be said about A? Is it rational? Irrational? There is a quick and short proof that it's not only transcendental, but also normal in base 3. Can you see it?
Note that the construction above can generate many similar sequences, depending on the image of the letter set {"0","{","}"} under R(w). To be exact, there are 10 letters ("0".."9") to choose from, so we can immediately construct (10 choose 3)=120 sequences. To generate additional sequences, we can reorder the elements inside Sn(0) in decreasing cardinality or in some other way. Since there are n! ways to arrange the elements inside each such set, this process can generate an infinity of additional sequences.
The Von Neumann Construction From a Metaphysical Perspective
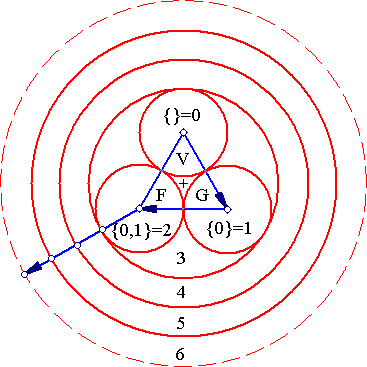
Let's take a little break from math now and examine the Von Neumann construct from a philosophical/metaphysical perspective. The Von Neumann construction is amazing in the sense that it requires only 3 elements: {"0","{","}"}. 0 is ultimately connected with emptiness and nothingness, a very basic characteristic of the universe. The two other symbols, "{" and "}" are ultimately connected with the properties of consciousness, separation and class. In a sense the first step of creation is consciousness "recognizing" the vast emptiness of space. As soon as this happens, the emptiness "separates" into "something" (that which has perceived the emptiness) and the emptiness itself. As soon as we have two things, a boundary is created: The 3rd element. The sequence thus is:
Note however that the (cardinality of the) set {0,{0}}=2 is not included in God's universe (2 not in {0,1}), therefore it implies a separate "existence" from that of 0 and 1. This existence/consciousness, the consciousness that corresponds to perceiving 2 (as a whole), or if you will, the consciousness that is 2, is The Firstborn[5][6].
Then, The Firstborn similarly claims: "All that exists (for now) is Void, God and Me" ({0,{0},{0,{0}}}=3). But again, the cardinality of the latter is not included in the previous universe! From that point on, the same thing happens with every new cardinality, so the moment God finishes step 3 above, we have an explosion or chain reaction of existences, which generates the first infinite hierarchy in existence: The first Big Bang: The Creation of The Natural Numbers! Tremendous![1][2][3][7][8][9]
The natural numbers in turn realize that their existence implies the existence of their negatives. The integers are created. The integers in their turn realize that their existence implies the existence of the rationals and so on and so forth. The irrationals are created. Then the reals. Then the complexes, the quaternions, the octonions, sedenions, vector spaces, fields, algebras, etc. The existence of Mathematics is established and its kingdom is set above all other kingdoms, except that of music (which is a direct creation of the rational numbers, therefore precede the reals).
The two most famous transcendental constants of mathematics for example are created directly from the Naturals as shown in the Yin-Yang symbol.
From that point on, it's a one way street: God now has a powerful tool at his disposal: Mathematics, with which He can generate pretty much all of reality and characterize existence down to any desirable detail by using Applied Mathematics to model it. The second Big-Bang occurs and the universe follows... The rest is history.
The whole construction is thus ultimately related to the three numbers {0,1,2}, and hence to the base 3 and the number 3. The numbers {0,1,2} therefore (or if you prefer the numbers {1,2,3}) form an archetype upon which all of reality stands. It is not a coincidence therefore that the number 3 is connected with various interesting facts:
It seems then that the Trinitarian dogma of 2 is a remnant (or evolute) of 1, so things are simpler than what the theologians make them to be. If we call V=Void, G=God, F=Firstborn, then the sequence above is described pictorially as: