A Simple Time Machine

Version 1.3 of 1/9/2020-11:33 a.m.

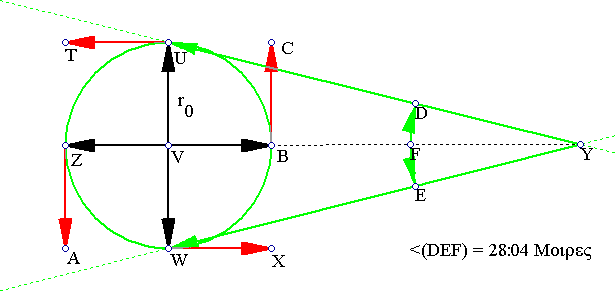
It is not accidental the setup on the article Using a Laser To Visualize Chaotic Turbulent Micro-Flow has been used in connection to time travel. The setup does indeed exhibit some interesting behavior which can be visualized easily. Consider the setup viewed side ways, as follows:

For a total spread angle DFE, the rotational movement of the laser beam gives rise to an angular frequency/velocity equal to ω=2*π/T. This in turn gives rise to a linear velocity v=ω*r, for the tip of the laser beam, which is realized at distance YV (as vectors UT, ZA, WX and BC).

Because v is a linear function of r, it follows that there is a r₀ and thus a specific YV, at which the linear velocity will become equal to c=3*10⁸m/s. This r₀ will be of course a function of the period T, as well. Assuming a fairly small T, such as the speed 10,000rpm which is the speed of some of the fastest car engines, we get T=3/500.

Solving the equation c=v=ω*r for r, we get r₀~286478.8m. Since r₀/YV=tan(DFE/2), we get: YV=r₀/tan(DFE/2), which for r₀~286478.8m and DFE/2=π/9 gives: YV~787094.3m

What all this means: If we had set this thingy up, with a laser mirror angle equal to 2*θ=π/9 for example, then at the distance of YV~787 km, where the radius of the sweep circle will be approximately r₀~286.5 km, we would get a 2D time-space singularity^[1] (a circle). To create a 3D singularity^[7], one needs to generalize the above in 3 dimensions, which can be done in at least two ways:

Mechanical

A mechanical time machine based on the above principle can be realized as a gyroscopic mechanism, with two rotating rings (green), anchored at AB and CD:

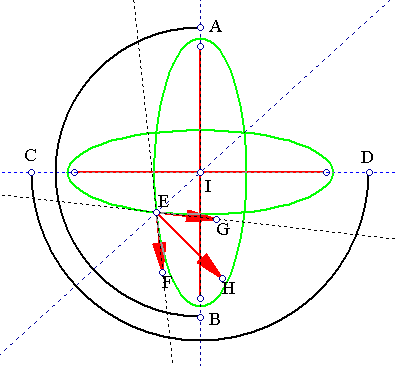
To create a singularity at E, the linear velocity there must be at least equal to c. Since the linear velocity EH is the sum of its components EG and EF, we must have: EG+EF=c. Because the two mechanical rings have (almost) the same diameter, we must have, r*sqrt(ω₁²+ω₂²)=c, from which we get the fundamental equation of the time machine with n=2 rings^[3]:

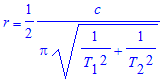
For a speed of 10000rpm for both rings, we get r~202.5km.

Optical

An optical time machine based on the above principle can be realized again as a gyroscopic mechanism, but this time instead of mechanical rings we can rotate laser beams. How many laser beams? To find out, we remember that any point on the surface of a sphere can be described by its Euler Angles, (α,β,γ). Further, if a point A is rotated to position E by the Euler angles (α,β,γ), it can be shown that there exist angles (a,b,c) such that the following list of operations rotates point A again to E^[4]:

1. Rotate by angle a around the z-axis.
2. Rotate by angle b around the new x-axis.
3. Rotate by angle c around the new z-axis.

Note that there are only two axes involved in the overall rotation when using angles (a,b,c). Therefore, we only need two rotating laser beams. Note also that this is equivalent to using one laser beam and two mirrors! A little judicious inspection shows that we can use the following mounting, as in the following figure^[5]:

Analysis

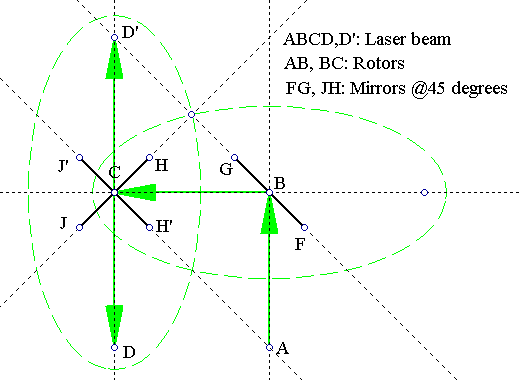
Choose the coordinate system to be that of Spherical coordinates. On the figure above then, denote as θ the angle of inclination and φ that of the azimuth. θ is realized as beam CD rotates around C and φ is realized as beam BC rotates around B (green ellipses).

For this setup then, if the rotation speeds of the two mirrors JH and GF have periods T₁ and T₂, then the equations for the two angles as functions of time t, are:

1. θ(t)=ω₁*t=2*π*t/T₁
2. φ(t)=ω₂*t=2*π*t/T₂

To create a 3D singularity then, the tip of the laser beam has to have a linear velocity v which satisfies the fundamental equation (above). And then, the phasor which describes the movement of the laser beam in 3-space as a function of time t, is given as:

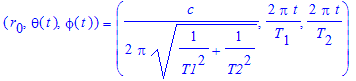
When this laser setup rotates fast enough, we will get a 3D (spherical) singularity at critical radius r₀. Plugging in some values, if the rotation speeds are 10000rpm, and 30000rpm, then T₁=60/10000, and T₂=60/30000, for which we get r₀~90.6km.

Time Dilation

The time for an observer inside the setup will be relativistically dilated and will be given as:

t'=t*γ=t/sqrt(1-(v/c)²)

where γ is now the Lorentz Factor. Note that v=r*sqrt(ω₁²+ω₂²), where r is the distance of the observer from B, hence the Lorentz factor becomes:

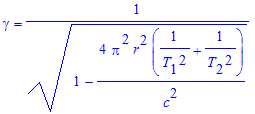
Follows a Maple graph of the relativistic time dilation for the above setup:

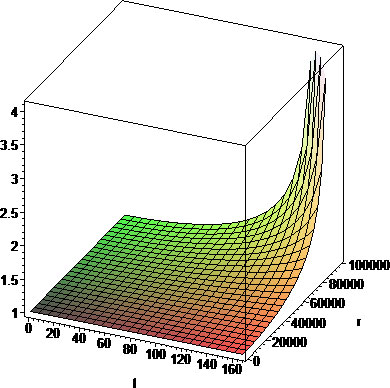
For example, at a distance of 90km, with rotation speeds of 10000rpm and 30000rpm, the Lorentz Factor will be γ~8.75. This means that for the observer inside the machine at this distance from the center, time passes at a rate 8.75 times faster than the time of an external observer. This means that the observer is moving into the future^[6].

Notes/References

1. For a relativistic explanation of what actually happens at YV (for pulsars), see pp. 268-274 of "Physics of Stellar Evolution and Cosmology", by H.S. Goldberg and M.D. Scadron, Gordon and Breach Science Publishers.
2. It is not accidental of course that this design is identical to the design of a simple gyroscope. The gyroscope is the dual of a time machine, since it detects any motion.
3. Note that this design is almost identical to the designs used in the films Contact and X-Men, although the radii of the mechanical rings used in these designs were way too small and n was not always equal to 2. Taking on average an r~50m and n=4 (as in the film Contact), we get T~0.2*10^-5s, which implies at least 477464.8rps or 477.4kHz for each of the rings. That's approximately 35.8 orders faster than the fastest rotor (ultrasonic dental drill) we have.
4. See for example, p. 161 of Scientific Programming With Macintosh Pascal, by R.E. Crandall and M. M. Colgrove, John Wiley & Sons, Inc.
5. Such an operating mounting bares an interesting resemblance to the scheme found in this page.
6. This was also the case in the film Contact, where Dr. Arroway experiences 18 hours of time to have been passed while inside the machine, relative to a few seconds for the external observers.
7. For a real-time effect of the first optical setup, consult video Time Relay in Chaotic Harmonic Oscillator, where the 3D singularity becomes visible close to the rotor, because of Rayleigh Scattering. For full details theoretical, consult ResearchGate.