All the spectroscopes described in the author's web pages either require effort to build or are expensive. There is however one alternative to those who wear nearsightedness eyeglasses: The Eyeglass Wearer's Spectroscope! If you are wearing fairly strong prescription myopia (or hypermetropia) glasses, then you are ready to see some spectra! Let's see how this spectroscope works:

Dispersion schematics for myopia lens

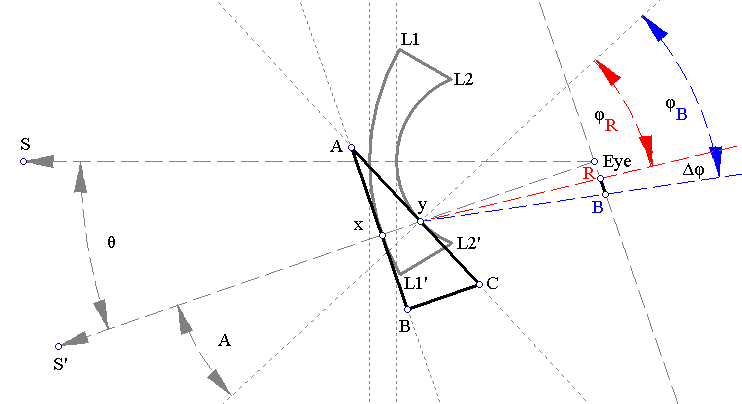
When an observer looks directly at a source S, the source's light travels along the optical axis of the eye-lens system which is perpendicular to the optical center of the lens L1-L2-L2'-L1'. Drawing the two tangents at the two lens surface points where the source's ray intersects the lens, we see that they are parallel; therefore there is no chromatic abberation, and hence no spectrum can be seen.

When the observer however looks at the same source through "the edge" of one's eyeglasses, things can become quite interesting! Looking at the source thus, amounts to rotating one's head by an angle θ around one's eye. When this happens, we can again trace the light ray, which now intersects the lens at x and y. Drawing the lens surface tangents at x and y, we see now that the tangents define a small triangle ABC.

The above means that for practical purposes when the observer looks at the source S' through the edge of one's eyeglass lens, one is looking at the source through a small prism ABC. But we know what happens when we look at sources through prisms! We get spectra!

The small prism ABC will then disperse the light ray of the source S', forming a mini spectrum, whose rays will deviate according to wavelength. Because blue deviates more and red less, blue wavelengths will tend to deviate towards C and red wavelengths will tend to deviate towards A.

The above means that if the source is small enough, it will decompose into a mini spectrum, whose blue part will be visible to the right (up in the figure) of the field of vision and the red part will be visible to the left (down in the figure) of the field of vision.

Analysis

Without loss of generality and to simplify the calculations, assume that the center of curvature of the lens' external surface is located exactly at the eye. This means that there is no deviation for the light ray at x. At y, however, we have the classic refraction situation, governed by the refraction law:

In our case we then have: sin(φ_R)/sin(A)=n_R and sin(φ_B)/sin(A)=n_B. The blue component of the rays will deviate more than the red component, consequently, a mini-spectrum RB will be projected onto the retina, whose width Δφ will be given exactly by:

The width of the produced spectrum therefore depends on the apical angle A of the triangle ABC and on the index of refraction of the lens.

Let us now analyze the above expression. We have two variables, n and A. In eyeglass prescriptions these two are dependent. I.e., for a specific prescription, the thickness of eyeglass lenses at the edges is naturally dependent on the material the lens is made of, and hence on n. To avoid going into such complicated details, we will assume first a constant angle A and then a constant lens material.

Here are the results for some popular optics glasses, using the following parameters: n_d: index of refraction at the He 587.6nm line. n_R: index of refraction at 660nm. n_B: index of refraction at the Hg 435.8nm line, v_d: Abbe Number and for A=10°.

Here are the widths Δφ when the material is kept constant and A varies. The vertical black line corresponds to A=10°, which gives the data above.

Δφ as a function of A, for 0° ≤ A ≤ 30°.
FS=red;BK7=green;BaK2=blue;BaK4=cyan;
IRGN=magenta;F2=aquamarine;SF10=yellow;LaSFN9=brown;

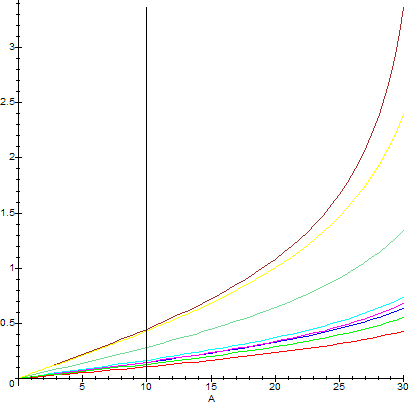
Several interesting conclusions can be deduced from the above two analyses. First, it is fairly obvious that as n increases, so does Δφ. The only anomaly that shows up violating this conclusion is the data for the IRGN glass. The reason why this glass deviates from the norm is easily explained however: Its Abbe Number is very high, which in turn means that this material has a relatively low dispersivity compared to its neighbors.

It is also fairly obvious that as A increases, Δφ also increases. This means that the "thicker" the lens edge is, the more visible the effect will be when the observer looks at the source through the edge. The asymptotic behavior of expression (1) for A close to zero is Δφ ~ (n_B-n_R)*A + O(A³), hence for small A, Δφ varies linearly with respect to A, which is also fairly obvious from the graph above.

A small source tends to produce a more visible spectrum, because then Δφ is large compared to the visual thickness of the source. The mini spectrum is fairly obvious with myopia eyeglasses of strength greater than or equal to 3-5 diopters. The mini spectrum gets produced with smaller prescriptions as well, but Δφ is small and therefore it is not as noticeable.

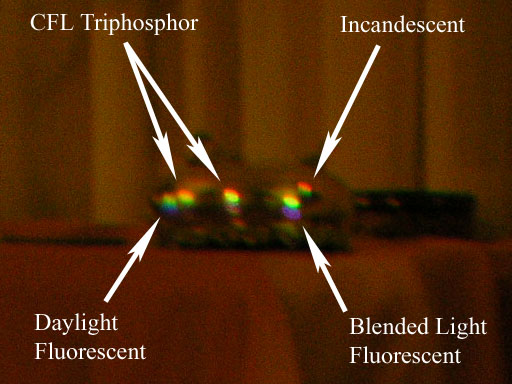
This mini-spectroscope is a virtually inexhaustible way to have fun examining the spectra of distant light sources at night, however, the author is aware of eyeglass wearers to whom this effect can be annoying and (according to their testimonies) potentially a source of headaches with certain triphosphor fluorescent lamps, such as with compact fluorescents (CFLs). According to them when they look at white objects illuminated by such lamps through the edges of their eyeglasses, they see two images of the object, one corresponding to the red 611nm peak and another corresponding to the green 546nm peak (see CFL spectra, below).

The effect tends to be exaggerated with light sources which contain emission lines separated by relatively large dark gaps in their emission spectra. Lamps which contain Mercury emissions for example, tend to exacerbate this effect even more (see blended light fluorescent spectrum, below).

WARNING: Don't engage this mini-spectroscope when you drive a vehicle at night, lest you want to find yourself landing in a hospital!

The spectacle spectroscope effect has been captured on camera using a special setting with the author's second pair of myopia eyeglasses, using a convex silver bowl to reflect four distant light sources: A small incandescent lamp, a blended light fluorescent lamp, two CFL triphosphor fluorescents and a daylight fluorescent:

Convex silver bowl reflecting four types of light sources.

Left myopia lens entering the scene from below.

Zooming in through the left "edge" of the myopia lens.
The mini spectra are already visible

The four different types of spectra produced by the author's eyeglass left myopia lens.

Part of the previous picture, magnified and processed with Photoshop to show specific spectral lines^[1].

Notes

1. To see these spectra in detailed form: Incandescent: [1.2.2]. Blended light fluorescent: [1.4.5]. CFL triphosphor: [1.3.3]. Daylight fluorescent: [1.3.1].