High Pressure sodium lamp discharge tube[8]
Types of Spectra
The physics of discharges is fairly complicated. Without going into too much detail, the spectra emitted fall under three categories:
The Self-Absorption Phenomenon
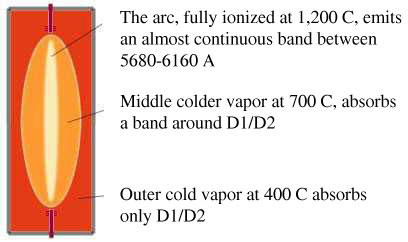
Unofficially, there is a fourth category, the mixed or degenerate kind, which are spectra which may contain linearity and continuity simultaneously (Na). In reality, whenever continuum is to be found around or close to certain lines in the emission spectrum, the phenomenon of self-reversal takes place. This phenomenon, otherwise known as spontaneous reversal or the corona phenomenon[1], occurs whenever more energy than the energy required to transition an electron is being provided- usually in ground transitions. Look at the figure below, depicting a simplistic schematic for a sodium discharge tube:

Now look at the self-absorption phenomenon as seen through the Phasmatron spectroscope, displaying precisely this behavior optically:
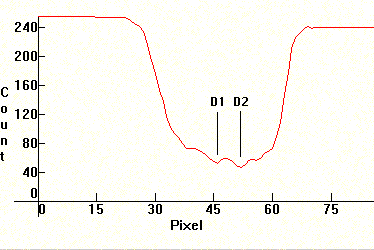 |
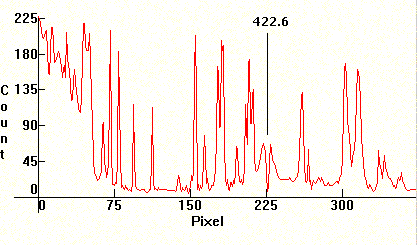
You can see the continuum emitted by the arc around the absorption band, and then the dark absorption band with the two Sodium lines in the middle. So the phenomenon actually occurs because Kirchoff absorption occurs inside the tube, along with continuous emission. A more detailed spectral distribution to the right shows clearly what's happening. The absorption that occurs on the D1/D2 doublet is clearly visible.
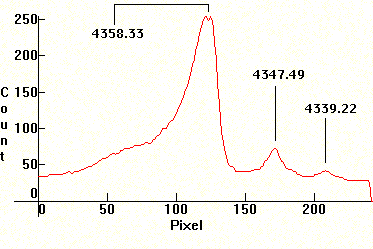
Self-absorption usually happens with resonance lines, i.e. with lines whose transitions terminate at the ground state. For example, the sodium D1/D2 lines above are resonance lines. However, when the density of the discharge plasma is high, enough absorption on the resonance lines causes self-absorption on other lines as well. Here is a similar absorption which happens on some of the visible lines of Mercury under high pressure, although less pronounced. This is the blue Mercury line, followed by the corresponding spectral distribution.
 |
As it happens on the main 253.7nm resonance line of Mercury under different conditions along with the corresponding distributions aligned. Note the emission peaks coinciding with the absorption centers:
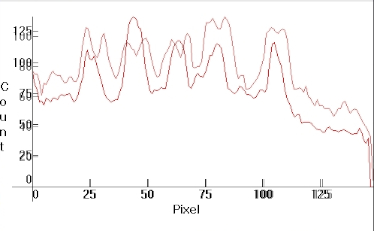 253.7nm line profile: Upper:hot discharge; lower:cold discharge (from: [1]) |
In general, most conventional discharge sources used for lighting exhibit this phenomenon, even on non-resonance lines, whenever the plasma pressure is high. Most of the times though, the spectroscopes are not powerful enough to show self-reversal because the width of the absorption within the line is of an order of a couple of Angstroms, sometimes even less than an Angstrom[2]. The second photo before the end in the Hg document (same as the one above), which shows the blue Mercury line, needs at least an R=50,000 to show the effect. The effect is less obvious as the ionization levels for a particular element go up in eV and as one moves to non-resonance lines. Sodium displays this behavior because it has a relatively low ionization energy level and because the D doublet is a resonance line. Mercury on the other hand needs much higher energies to show this effect on its visible lines which are not main resonance lines. In any case, alkali are prone to showing the effect on relatively low power spectroscopes, as are some easily ionizable metals. The effect can be seen on Li, Ca and sodium sometimes using an R as low as 700-800. For color photographs which show this effect, consult The Double Amici Prism Hand-Held Spectroscope[3].
Approximating the Profile of Lines Suffering Self-absorption[8]
The light distribution around the emission wavelength of specific lines can be approximated using the Lorentzian distribution. Let's use Maple to try to approximate the complete profile of the phenomenon as a function of time for the High Pressure Sodium Lamp. We start with the basics:
> restart;
> with(plots):
> K:=C->C+273.15;#Celsius -> Kelvin
> C:=K->K-273.15;#Kelvin -> Celsius
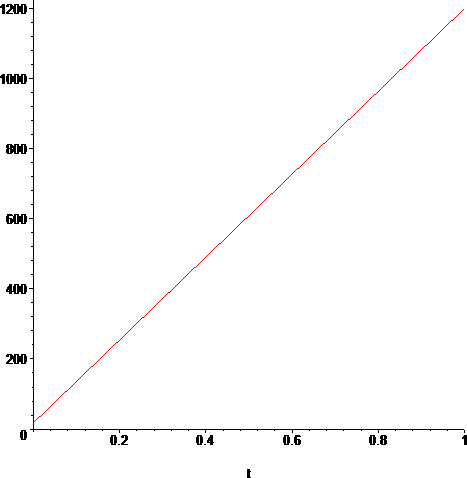
[3] gives the temperature of the hottest spot of the discharge tube of this lamp, as 1200°C. The usable temperature range therefore, is 18°C-1200°C.
> t0:=0;#start time
> t1:=1;#end time
> Tr:=K(18);#T radiating in K
> Ti:=K(1200);#T ionization in K
> eq:=(T-Tr)/(t-t0)=(Ti-Tr)/(t1-t0);#equation of temperature as function of time
> T:=unapply(solve(eq,T),t);#solve as a function of our t
Check:
> C(T(t0)),C(T(t1));
18.0000000, 1200.000000
> plot(C(T(t)),t=t0..t1);
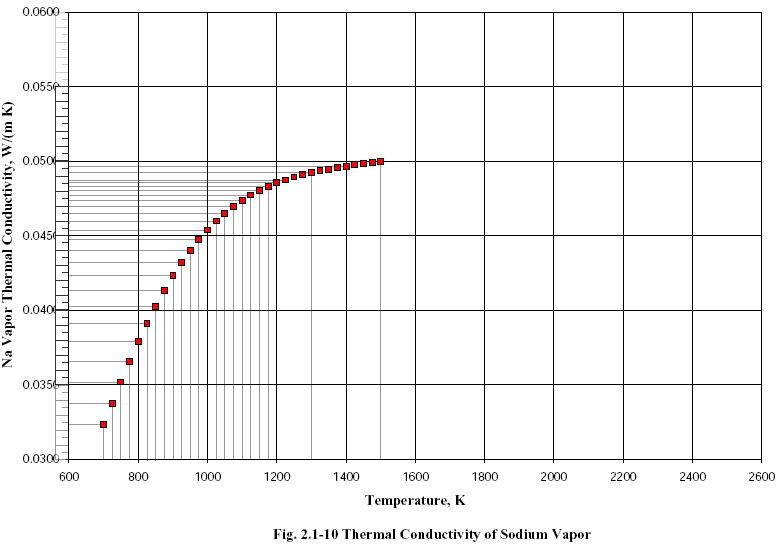
Now we need the Thermal Conductivity for sodium vapor. We consult "Thermal Transport" document in [4] and we get a small table for the Thermal Conductivity of sodium vapor, which we re-measure carefully[4].
The data is measured and put in a list which we can manipulate with Maple:
> with(CurveFitting):
> LT:=[seq(700+n*100,n=0..8)];#temperatures
LT := [700, 800, 900, 1000, 1100, 1200, 1300, 1400, 1500]
> s:=(0.0350-0.030)/10;#temp step size
> Ld:=[4.9,15,24.5,30.5,34.8,37.2,38.5,39.2,40];#chart measure in steps
Ld := [4.9, 15, 24.5, 30.5, 34.8, 37.2, 38.5, 39.2, 40]
> Lk:=[seq(0.030+Ld[n]*s,n=1..nops(Ld))]:#store conductivity as a list
> k:=unapply(PolynomialInterpolation(LT, Lk,T),T):#find interpolating polynomial for data
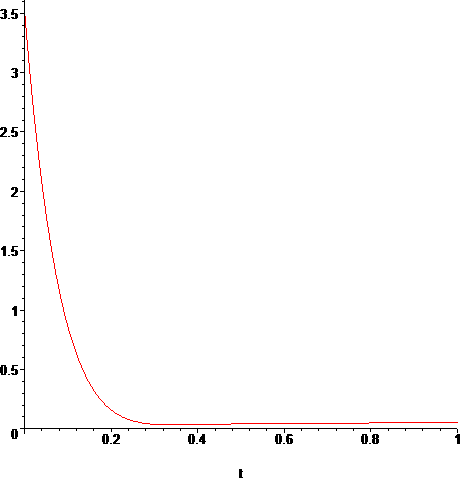
The sodium vapor Thermal Conductivity data is available only for the range 700°K-1500°K. This corresponds to 426.85°C-1226.85°C. Ti=T(t1) falls inside this range, so we are ok on this, but T(t0)=Tr does not. There's nothing we can do about that, so we will just use the resulting interpolating polynomial as we get it from the data[5]. The resulting interpolating polynomial is:
> plot(k(T(t)),t=t0..t1);
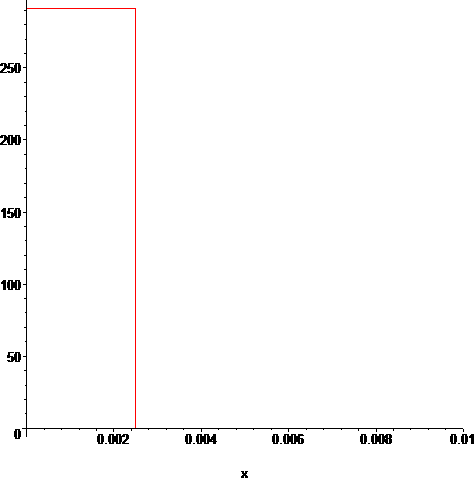
Next we need to model the High Pressure Sodium lamp inner discharge tube. How do we do that? In the most obvious way. As an energy pulse of thickness equal to the tube thickness. The inner discharge tube has an average thickness of 5/1000, so,
> H:=Heaviside;
> g:=unapply(piecewise(x<=2.5/1000,T(t)),x,t);#half thickness 2.5/1000
> plot(g(x,0),x=0..10/1000);#tube temp @t0
The problem is now a simple Heat Equation problem. Specifically, we are dealing with the solution for the homogeneous case (sodium vapor throughout), so the general solution is given in terms of the Thermal Conductivity of sodium vapor k(T(t)) (which we have, above) as:
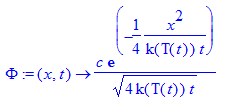
> c:='c';#normalization constant
> Phi:=(x,t)->c/sqrt(4*k(T(t))*t)*exp(-x^2/(4*k(T(t))*t));#solution for homogeneous Heat Equation
> u:=unapply(int(Phi(x-y,t)*g(y,t0),y=0..1),x,t):#convolute
> c:=solve(int(Phi(x,t0+1e-10),x=0..1)=1/2,c);#normalize
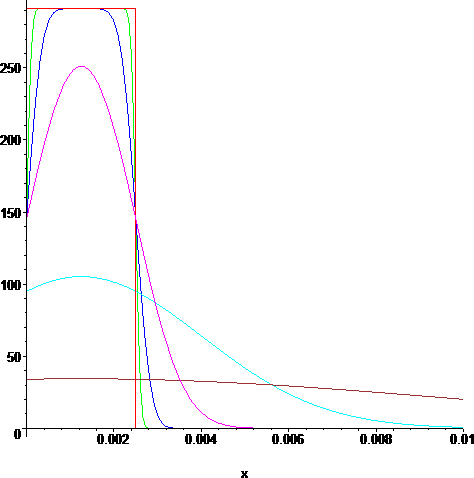
> p1:=plot(g(x,0),x=0..10/1000,color=red):
> p2:=plot(u(x,1/(10^9)),x=0..10/1000,color=green):
> p3:=plot(u(x,1/(10^8)),x=0..10/1000,color=blue):
> p4:=plot(u(x,1/(10^7)),x=0..10/1000,color=magenta):
> p5:=plot(u(x,1/(10^6)),x=0..10/1000,color=cyan):
> p6:=plot(u(x,1/(10^5)),x=0..10/1000,color=brown):
> display({p1,p2,p3,p4,p5,p6});
We are done with the preliminaries. We now approximate the Lorentzian profile of an emission line[6]:
> Lp:=(w,w0,gamma)->1/(1+((w-w0)/gamma)^2);#Lorentzian distribution
> L:=proc(T1,T2,wr)
> local s;
> if T2<=Tb then #if T2 of outer vapor less than Tb, show just emission
> s:=plot(Lp(w,0,(T1-Tr)/(Ti-Tr)),w=-wr..wr);
> else #if T2 of outer vapor greater than Tb, then we have absorption!
> s:=plot(Lp(w,0,(T1-Tr)/(Ti-Tr))-Lp(w,0,(T2-Tb)/(Ti-Tb)),w=-wr..wr);
> fi;
> s;
> end:
Now we approximate the behavior as a function of time for all temperatures between t0 and t1:
> N:=30;
> dt:=(t1-t0)/N;
> u:='u';u:=array(0..N):
> for n from 0 to N do
> c:='c';Phi:='Phi';Phi:=(x,t)->c/sqrt(4*k(T(t))*t)*exp(-x^2/(4*k(T(t))*t));
> u[n]:=unapply(int(Phi(x-y,t)*g(y,t0+n*dt),y=0..1),x,t):
> c:=solve(int(Phi(x,t0+n*dt+1e-10),x=0..1)=1/2,c);
> od:
> LP:=[seq(L(T(t0+n*dt),u[n](1.25/1000,t0+8e-8),15),n=1..N)]:#animation list
> for n from N+1 to N+15 do
> LP:=[op(LP),L(T(t0+N*dt),u[N](1.25/1000,t0+8e-8),15)];#add some extra frames
> od:
> display(LP,insequence=true);
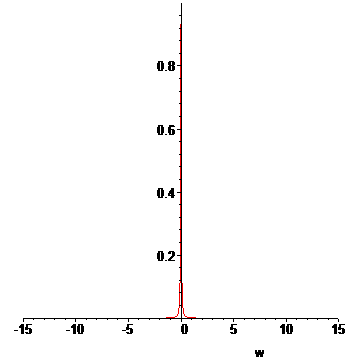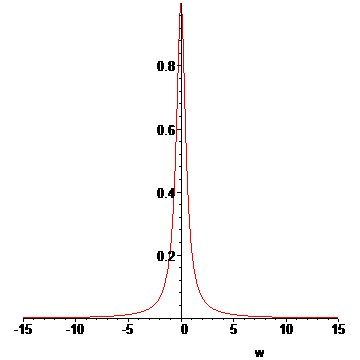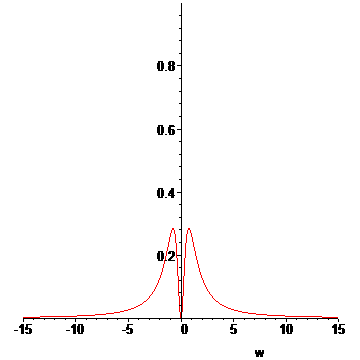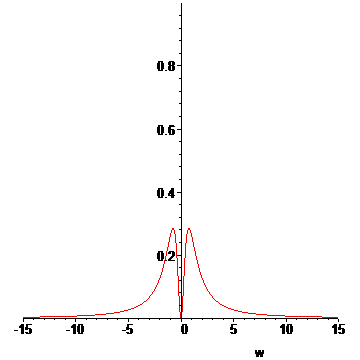
 |